The disc of radius r is confined to roll without slipping at A and B. If the plates have the velocities shown, then
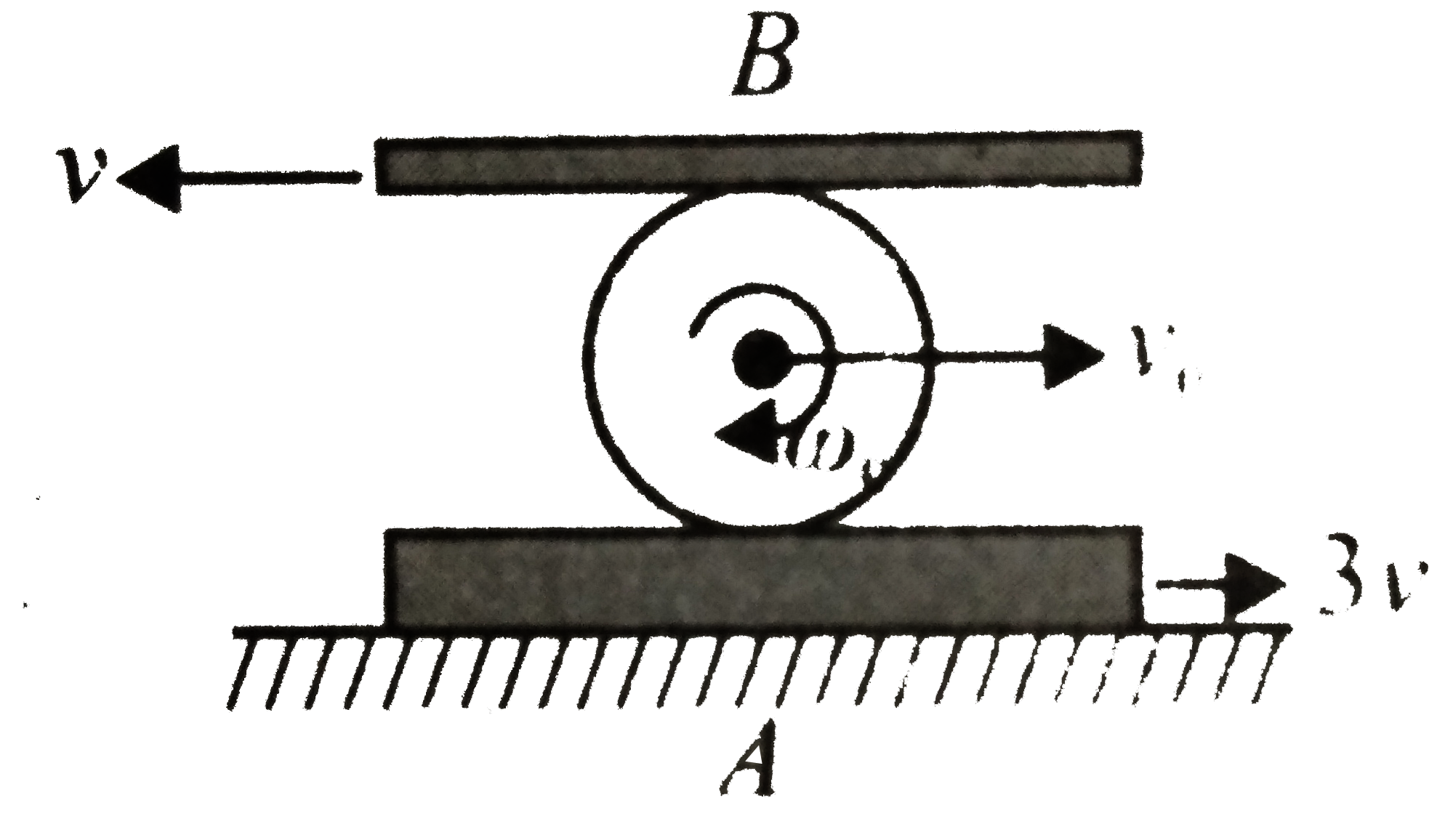
angular velocity of the disc is 2V/r
linear velocity V0=V
angular velocity of the disc is 3V/2r
none of these
The correct Answer is:A, B
v0=rω0=3v……i
v0+rω0=−v….ii
From eqn i and ii we get
2v0=2v⇒v0=v
v0+v0=−rω0⇒ω=2vr
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
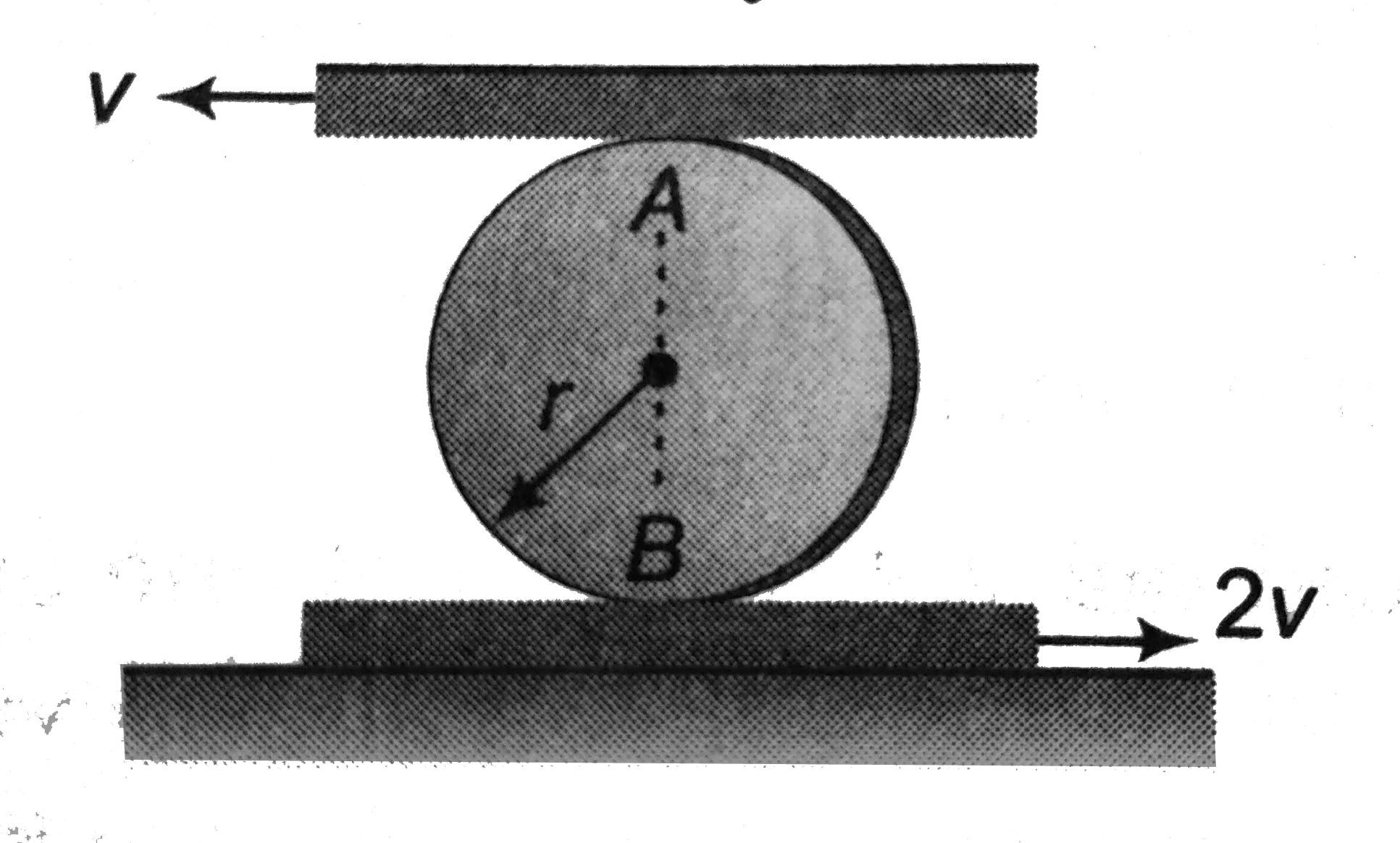
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is

View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View Solution
A cylinder of radius R is to roll without slipping between two planks as shown in the figure. Then
View SolutionIf a rigid body rolls on a surface without slipping, then:
View SolutionA disc of radius 20CM is rolling without slipping on a flat horizontal surface. At a certain instant the velocity of its centre is 4m/s and its angular velocity is 10rad/s. The lowest contact point is O.
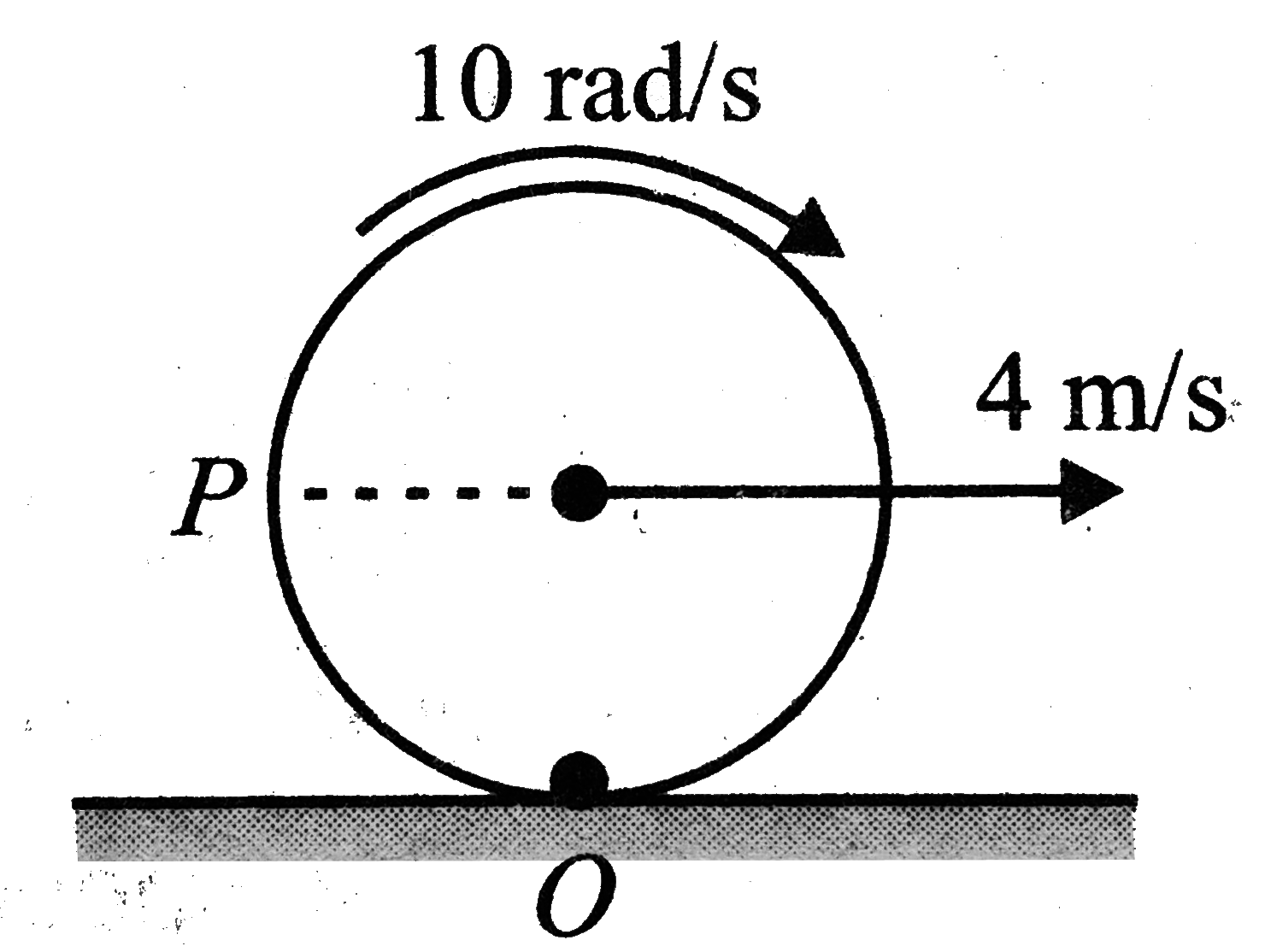
Velocity of point P is
View SolutionA disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.

Speed of point P having coordinates (x,y) is
View SolutionA disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown.
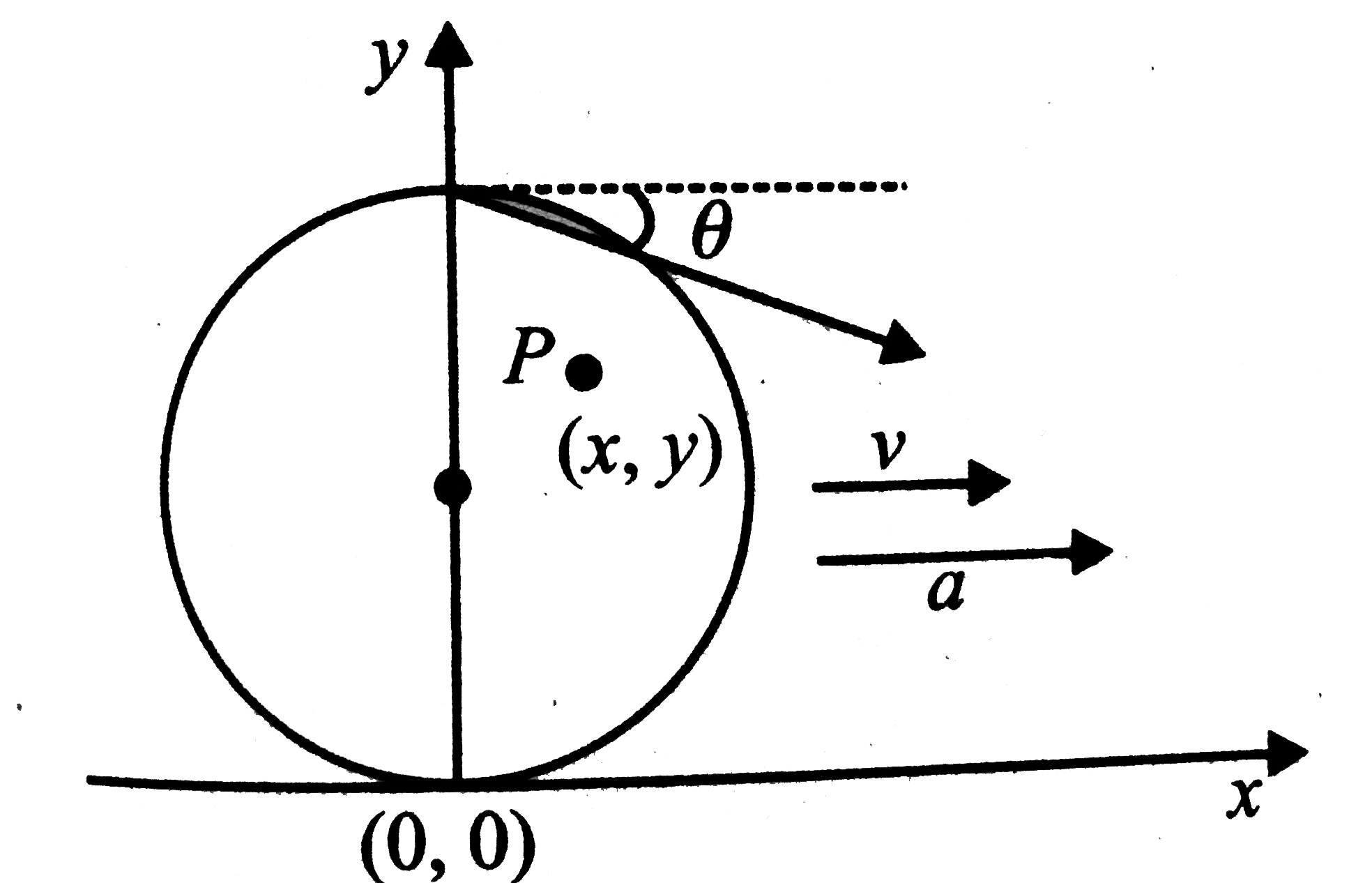
If v=√2aR the angle θ between acceleration of the top most point and the horizontal is
View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View Solution
