A disc having radius $R$ is rolling without slipping on a horizontal ( $x - z$ ) plane. Centre of the disc has a velocity $v$ and acceleration $a$ as shown.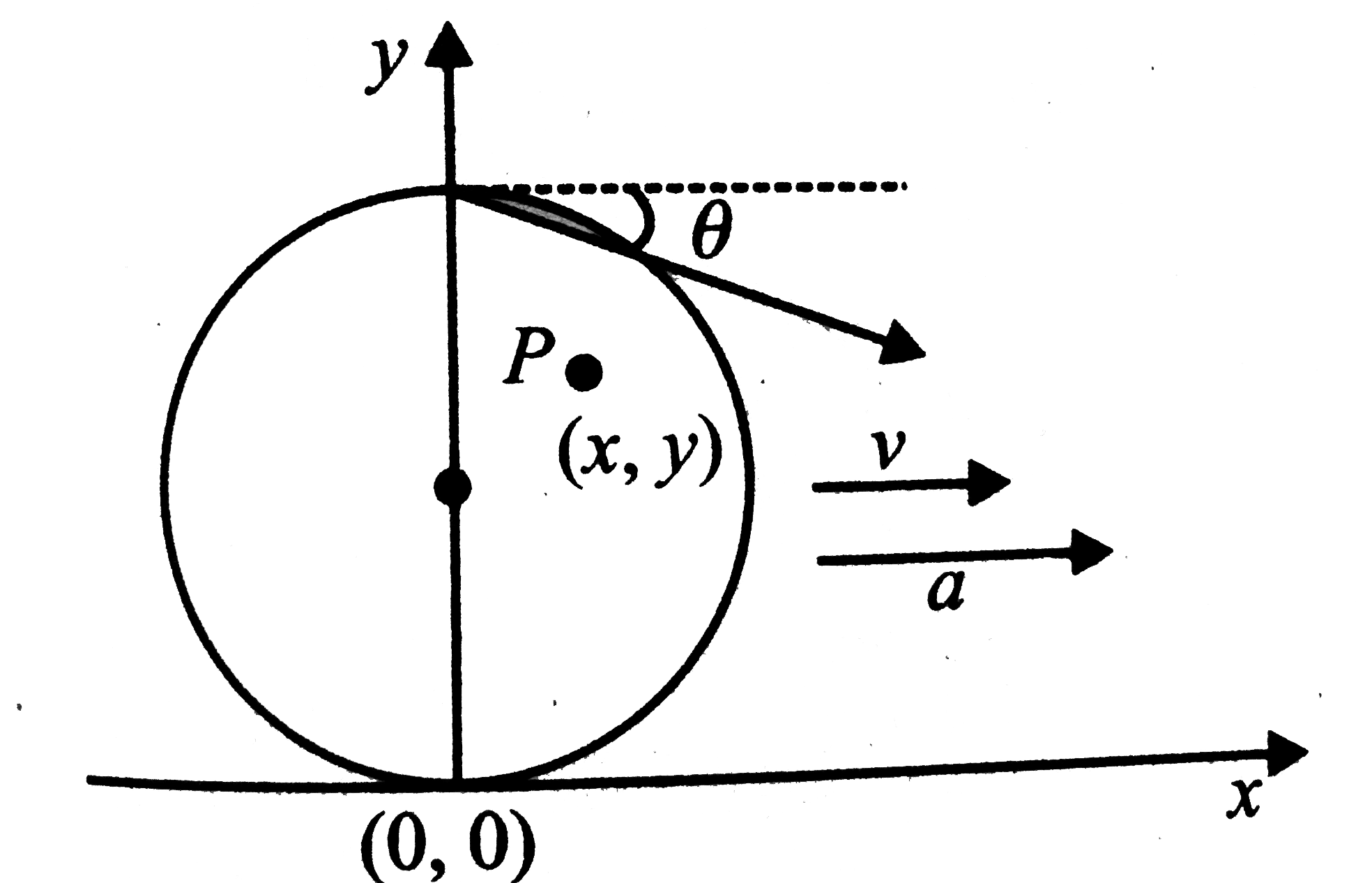
If $v = \sqrt{2 a R}$ the angle $θ$ between acceleration of the top most point and the horizontal is

$0$

$45^{\circ}$

${tan}^{- 1} 2$

${tan}^{- 1} (\frac{1}{2})$

Video Solution

Text Solution

Verified by Experts

$a = α R$

$a_{C} = ω^{2} R = {(\frac{v}{R})}^{2} = \frac{v^{2}}{R} = \frac{2 a R}{R} = 2 a$
$tan θ = \frac{2 a}{2 a} = 1 \Rightarrow θ = 45^{\circ}$

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos

Knowledge Check

A solid cylinder of mass $M$ and radius $R$ rolls without slipping down an inclined plane making an angle $6$ with the horizontal. Then its acceleration is.
A1/3 g sin $θ$
B2/3 g sin $θ$
C2/5 g sin $θ$
D2/7 g sin $θ$

A wheel is rolling on a horizontal plane. At a certain instant it has a velocity $v$ and acceleration $a$ of $C M$ as shown in figure . Acceleration of

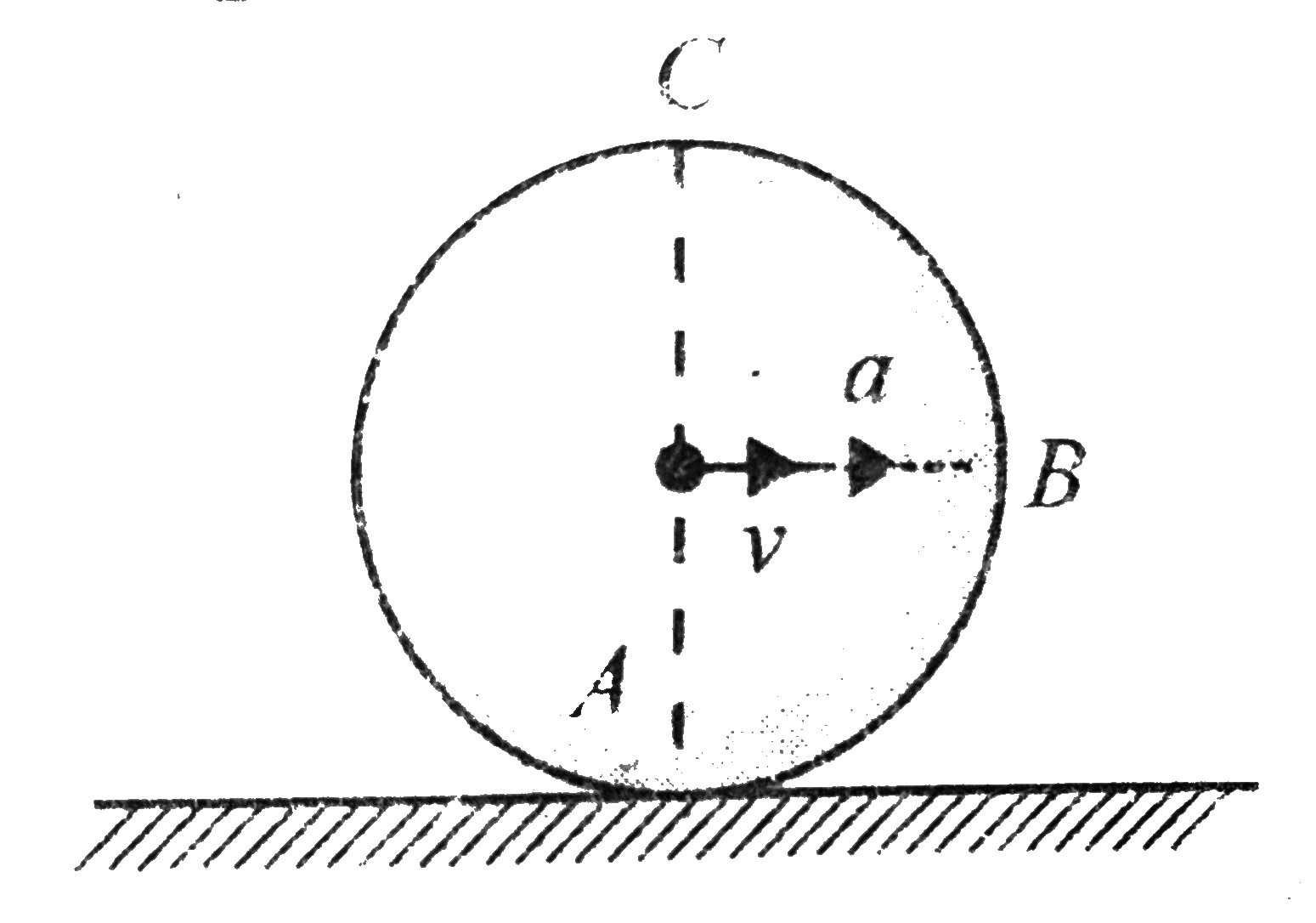
View Solution
A disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is $(O P = \frac{R}{2})$
View Solution
The disc of radius $r$ is confined to roll without slipping at $A$ and $B$ . If the plates have the velocities shown, then

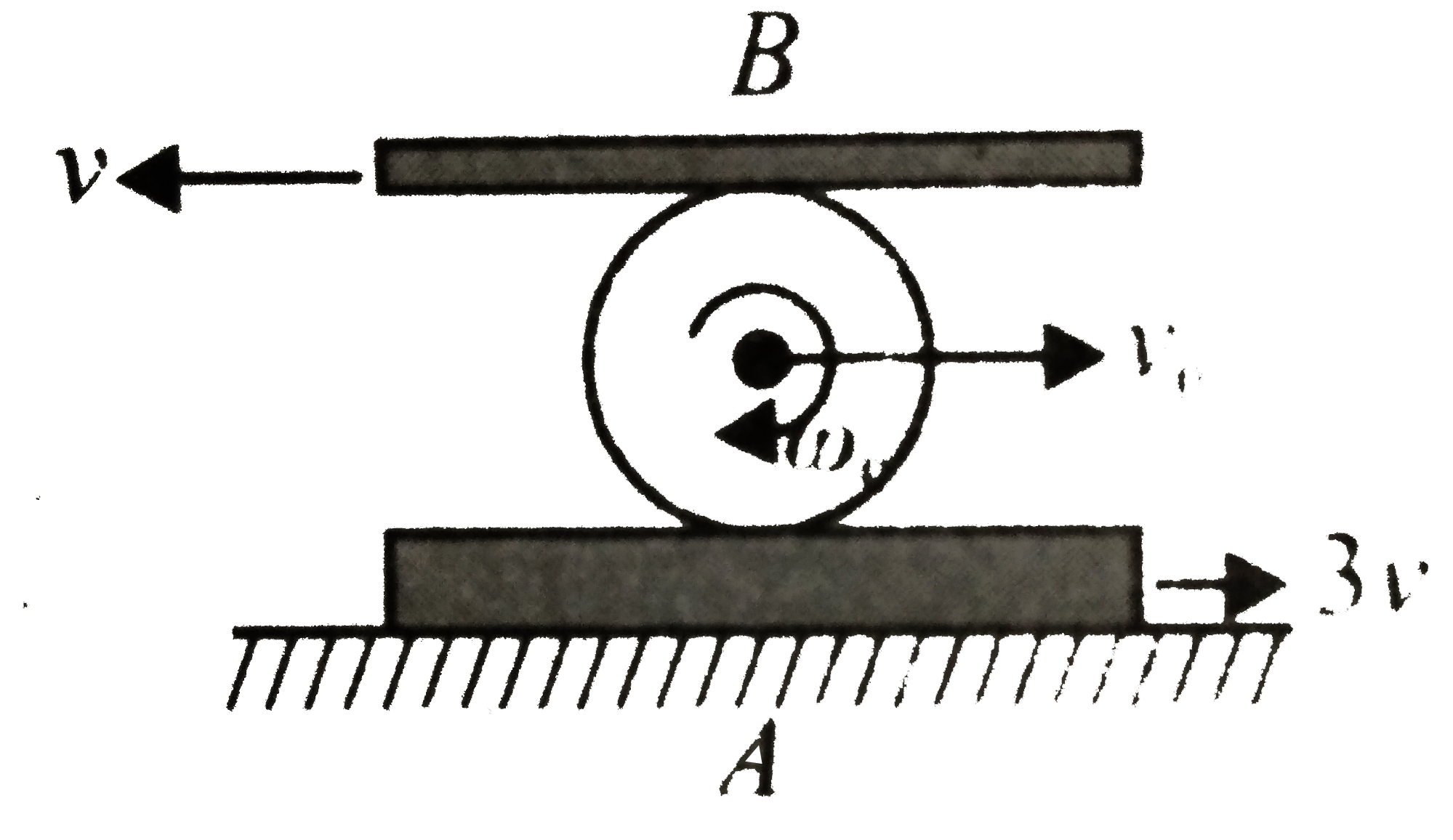
View Solution
A disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is

View Solution
A disc of radius $R$ is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point $P$ is
View Solution
A disc of radius $R$ is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point $P$ is

View Solution
A rolling object rolls without slipping down an inclined plane (angle of inclination $θ$ ), then the minimum acceleration it can have is ?
View Solution

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Linked Comprehension

An L shaped uniform rod of mass 2M and length 2L (AB = BC = L) is held...
05:45
A uniform rod of length L and mass M is lying on a frictionless horizo...
04:21
A uniform rod of length L and mass M is lying on a frictionless horizo...
04:21
A uniform rod of length L and mass M is lying on a frictionless horizo...
07:55
A bicycle has pedal rods of length 16 cm connected to sprocketed disc ...
03:23
A bicycle has pedal rods of length 16 cm connected to sprocketed disc ...
03:26
A bicycle has pedal rods of length 16 cm connected to sprocketed disc ...
02:13
A bicycle has pedal rods of length 16 cm connected to sprocketed disc ...
03:26
A bicycle has pedal rods of length 16 cm connected to sprocketed disc ...
03:22
A cord is wound round the circumference of a solid cylinder radius R a...
02:45
A cord is wound round the circumference of a solid cylinder radius R a...
02:45
A diving board 3.00 m long is supported at a point 1.00 m from the end...
01:14
A diving board 3.00 m long is supported at a point 1.00 m from the end...
03:15
The horizontal beam in figure weighs 150 N, and its centre of gravity ...
00:57
The horizontal beam in figure weighs 150 N, and its centre of gravity ...
05:22
A uniform ladder 5.0 m long rests against a frictionless, vertical wal...
08:04
A uniform ladder 5.0 m long rests against a frictionless, vertical wal...
08:04
A uniform ladder 5.0 m long rests against a frictionless, vertical wal...
08:04
A disc of radius R rolls without slipping at spped v along positve x-a...
03:32
A disc having radius R is rolling without slipping on a horizontal (x-...
02:24

Home
Ask Doubt
Profile

A disc having radius R is rolling without slipping on a horizontal (x−z) plane. Centre of the disc has a velocity v and acceleration a as shown. If v=√2aR the angle θ between acceleration of the top most point and the horizontal is

a=αR aC=ω2R=(vR)2=v2R=2aRR=2a tanθ=2a2a=1⇒θ=45∘

Topper's Solved these Questions

Similar Questions

Knowledge Check

A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 1-Linked Comprehension

A disc having radius $R$ is rolling without slipping on a horizontal ( $x - z$ ) plane. Centre of the disc has a velocity $v$ and acceleration $a$ as shown.
If $v = \sqrt{2 a R}$ the angle $θ$ between acceleration of the top most point and the horizontal is

$a = α R$

$a_{C} = ω^{2} R = {(\frac{v}{R})}^{2} = \frac{v^{2}}{R} = \frac{2 a R}{R} = 2 a$
$tan θ = \frac{2 a}{2 a} = 1 \Rightarrow θ = 45^{\circ}$

A solid cylinder of mass $M$ and radius $R$ rolls without slipping down an inclined plane making an angle $6$ with the horizontal. Then its acceleration is.