A uniform rod of length L and mass M is lying on a frictionless horizontal plane and is pivoted at one of its ends as shown in Fig. There is no friction at the pivot. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and impulse J acts for a small time interval △t. Now answer the following questions:

Find the impulse acted on the ball during the time △t
A. N3J(m+3M)L
B. 6J(m+3M)L
C. 3J(3m+M)L
D. 6J(3m+M)L
The correct Answer is:B
Let the system starts with agular velocity ω. Angular velocity if the ball will also be ω as it remais struck to the rod.

Velocity of the ball v=ωL3
For the rod angular impulse= change in angular momentum:
J2L3−JbL3=ML23ω.....i
For the ball, impulse = change in linear momentum
Jb=mv=mω(L3)......ii
From eqn i and ii ω=6J(m+3M)L
and Jb=2mJ(m+3M)

Let impulse on the pivot be J1
For the rod and ball system total impulse = change in linear
mometum J+J=Mvc+mv
Solve to get J1=mJm+3M
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A uniform rod of length L and mass M is lying on a frictionless horizontal plane and is pivoted at one of its ends as shown in Fig. There is no friction at the pivot. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and impulse J acts for a small time interval △t. Now answer the following questions:

Find the magnitude of the impulse applied on the pivot during the time interval △tView Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling isView SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 View Solution
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:
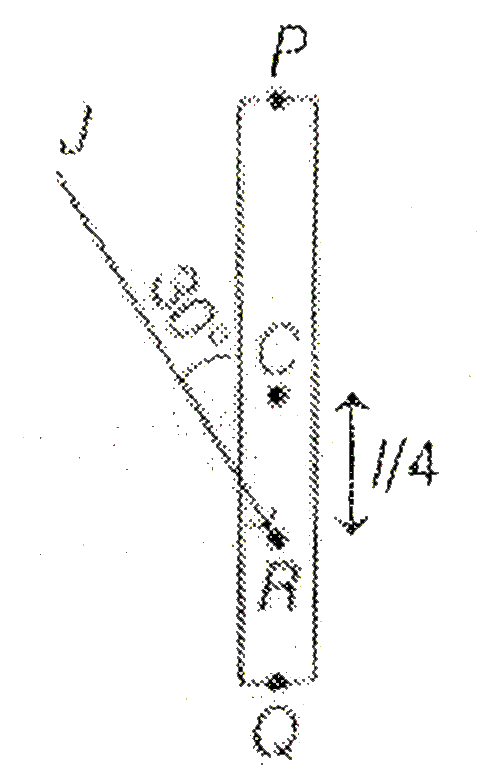
 View Solution
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 View Solution
View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
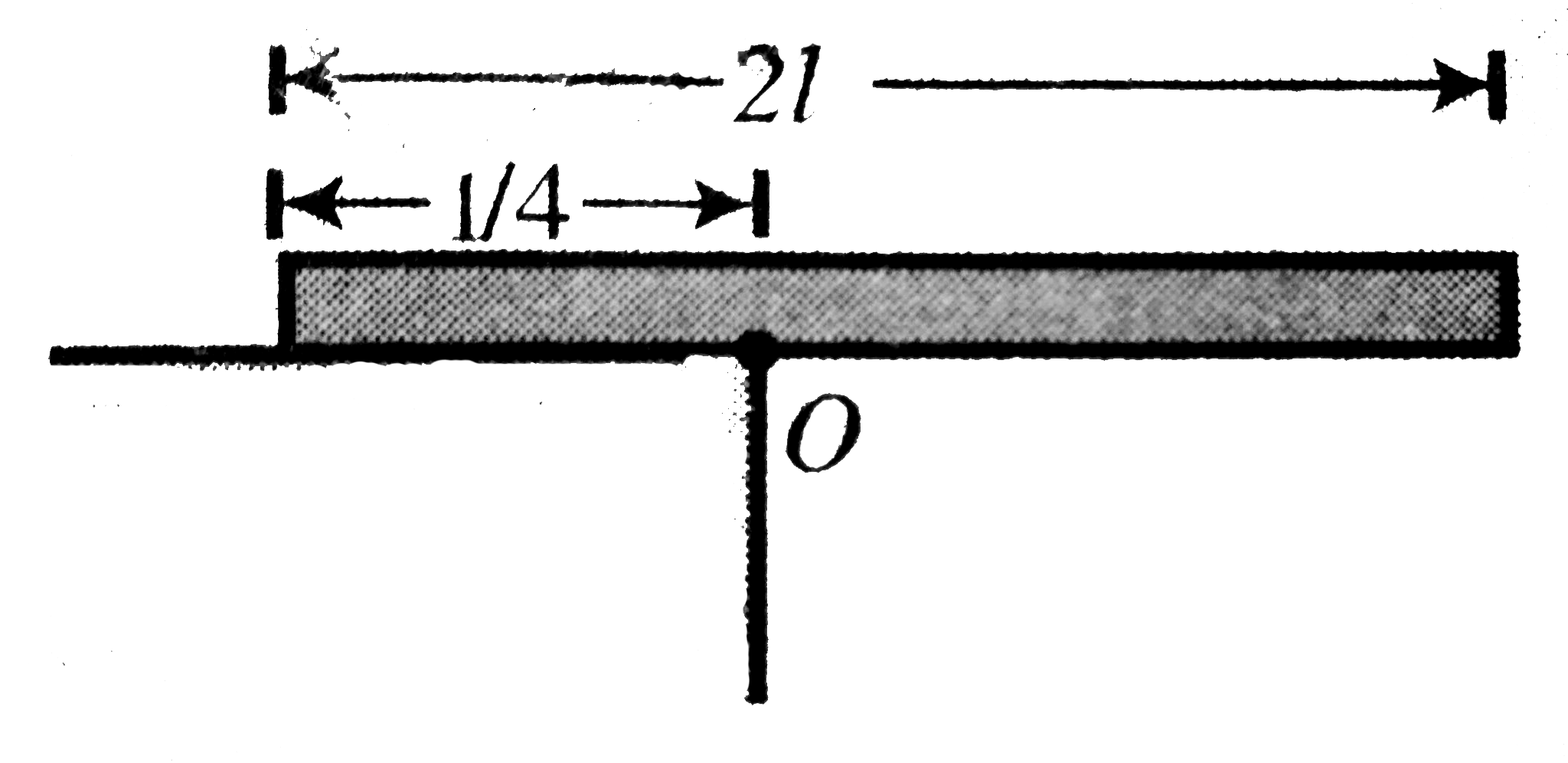 View Solution
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View Solution
