Question

One fourth length of a uniform rod of length $2l$ and mass $m$ is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.

Explanation

The torque applied by gravity about the edge `O=tau=mg(3/4)`

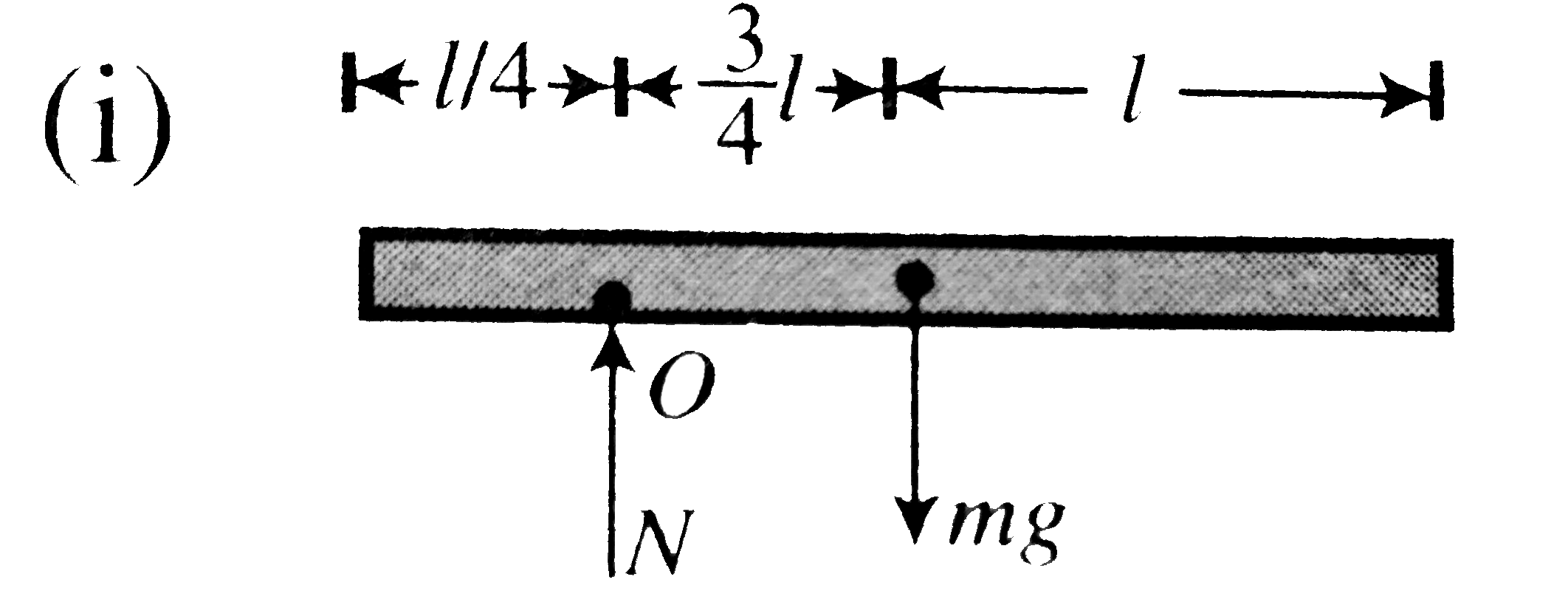
`impliesI_(0)alpha=3/4mg` ………i
where `I_(0)=I_(g)+m((3l)/4)^(2)`
`=(ml^(2))/12+9/16ml^(2)=(ml^(2))/4(1/3+9/4)`
`I_(0)=(31ml^(2))/48` ............... ii
i and ii yield `alpha =(3mg/4)/(31ml^(2)/48)`
`implies alpha=(144g)/(124l)=(36g)/(31l)`......iii
Newton's second law of motion.
`mg-N=ma`........iv
Kinematics `a=((3l)/4)alpha=(36g)/31` ..............v
`N=mg-m((27g)/31)impliesN=(4mg)/27`