Determine the minimum coefficient of friction between a thin rod and a floor at which a person can slowly lift the rod from the floor, without slipping, to the vertical position applying at its end a force always perpendicular to its length.
To solve the problem of determining the minimum coefficient of friction between a thin rod and a floor at which a person can slowly lift the rod from the floor to the vertical position, we can follow these steps:
1. Understanding the Setup:
- We have a thin rod lying on the floor. A force F is applied at the end of the rod, perpendicular to its length, to lift it vertically.
- The rod has a mass m and experiences gravitational force mg acting downwards.
2. Drawing the Free Body Diagram:
- Draw the rod horizontally on the floor.
- Mark the point where the force F is applied at one end.
- Indicate the normal force N acting upwards from the floor and the weight mg acting downwards at the center of the rod.
- The angle θ is formed between the rod and the vertical as it is being lifted.
3. Applying Newton's Laws:
- Since the rod is moving slowly and there is no acceleration, we can apply Newton's first law.
- In the horizontal direction (x-axis), the forces must balance:
F−Fsinθ=0⟹F=Fsinθ
- In the vertical direction (y-axis), the forces also balance:
N+Fcosθ=mg
4. Torque Calculation:
- To find the torque about the point where the rod touches the floor, we consider the torque due to the applied force and the weight of the rod.
- The torque due to the force F is FL (where L is the length of the rod), and the torque due to the weight mg is mg⋅L2cosθ.
- Setting the net torque to zero (for equilibrium):
FL−mg⋅L2cosθ=0
5. Solving for the Force F:
- Rearranging the torque equation gives:
F=mg⋅L2cosθL=mgcosθ2
6. Friction Condition:
- The condition for no slipping is given by:
f≤μN
- Here, the frictional force f can be expressed as:
f=Fsinθ=mgcosθ2sinθ
7. Substituting for Normal Force N:
- From the vertical force balance, we have:
N=mg−Fcosθ=mg−mgcos2θ2=mg(1−cos2θ2)
8. Finding the Coefficient of Friction μ:
- Substitute f and N into the friction condition:
mgcosθ2sinθ≤μ⋅mg(1−cos2θ2)
- Dividing through by mg (assuming mg≠0):
cosθ2sinθ≤μ(1−cos2θ2)
9. Rearranging to Solve for μ:
- Rearranging gives:
μ≥cosθ2sinθ1−cos2θ2
10. Final Expression:
- This expression gives the minimum coefficient of friction required to lift the rod without slipping.
- We have a thin rod lying on the floor. A force F is applied at the end of the rod, perpendicular to its length, to lift it vertically.
- The rod has a mass m and experiences gravitational force mg acting downwards.
- Draw the rod horizontally on the floor.
- Mark the point where the force F is applied at one end.
- Indicate the normal force N acting upwards from the floor and the weight mg acting downwards at the center of the rod.
- The angle θ is formed between the rod and the vertical as it is being lifted.
- Since the rod is moving slowly and there is no acceleration, we can apply Newton's first law.
- In the horizontal direction (x-axis), the forces must balance:
F−Fsinθ=0⟹F=Fsinθ
- In the vertical direction (y-axis), the forces also balance:
N+Fcosθ=mg
- To find the torque about the point where the rod touches the floor, we consider the torque due to the applied force and the weight of the rod.
- The torque due to the force F is FL (where L is the length of the rod), and the torque due to the weight mg is mg⋅L2cosθ.
- Setting the net torque to zero (for equilibrium):
FL−mg⋅L2cosθ=0
- Rearranging the torque equation gives:
F=mg⋅L2cosθL=mgcosθ2
- The condition for no slipping is given by:
f≤μN
- Here, the frictional force f can be expressed as:
f=Fsinθ=mgcosθ2sinθ
- From the vertical force balance, we have:
N=mg−Fcosθ=mg−mgcos2θ2=mg(1−cos2θ2)
- Substitute f and N into the friction condition:
mgcosθ2sinθ≤μ⋅mg(1−cos2θ2)
- Dividing through by mg (assuming mg≠0):
cosθ2sinθ≤μ(1−cos2θ2)
- Rearranging gives:
μ≥cosθ2sinθ1−cos2θ2
- This expression gives the minimum coefficient of friction required to lift the rod without slipping.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.2
17 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionA block of mass m is stationary on a rough inclined plane making an angle θ with the horizontal. Find the contact force between block and the plane
View Solution
Knowledge Check
The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g=10ms−2)
A2ms−2B4ms−2C6ms−2D8ms−2A crate of mass 100 kg is at rest on a horizontal floor. The coefficient of static friction between the crate and the floor is 0.4, and the coefficient of kinetic friction is 0.3 . A force F of magnitude 344 N is then applied to the crate, parallel to the floor. Which of the following is true ?
AThe crate will accelerate across the floor at 0.5m/s2.BThe static friction force, which is the reaction force to F as guaranteed by Newton 's Third Law, will also have a magnitude of 344 N.CThe crate will slide across the floor at a constant speed of 0.5m/s.DThe crate will not move.
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
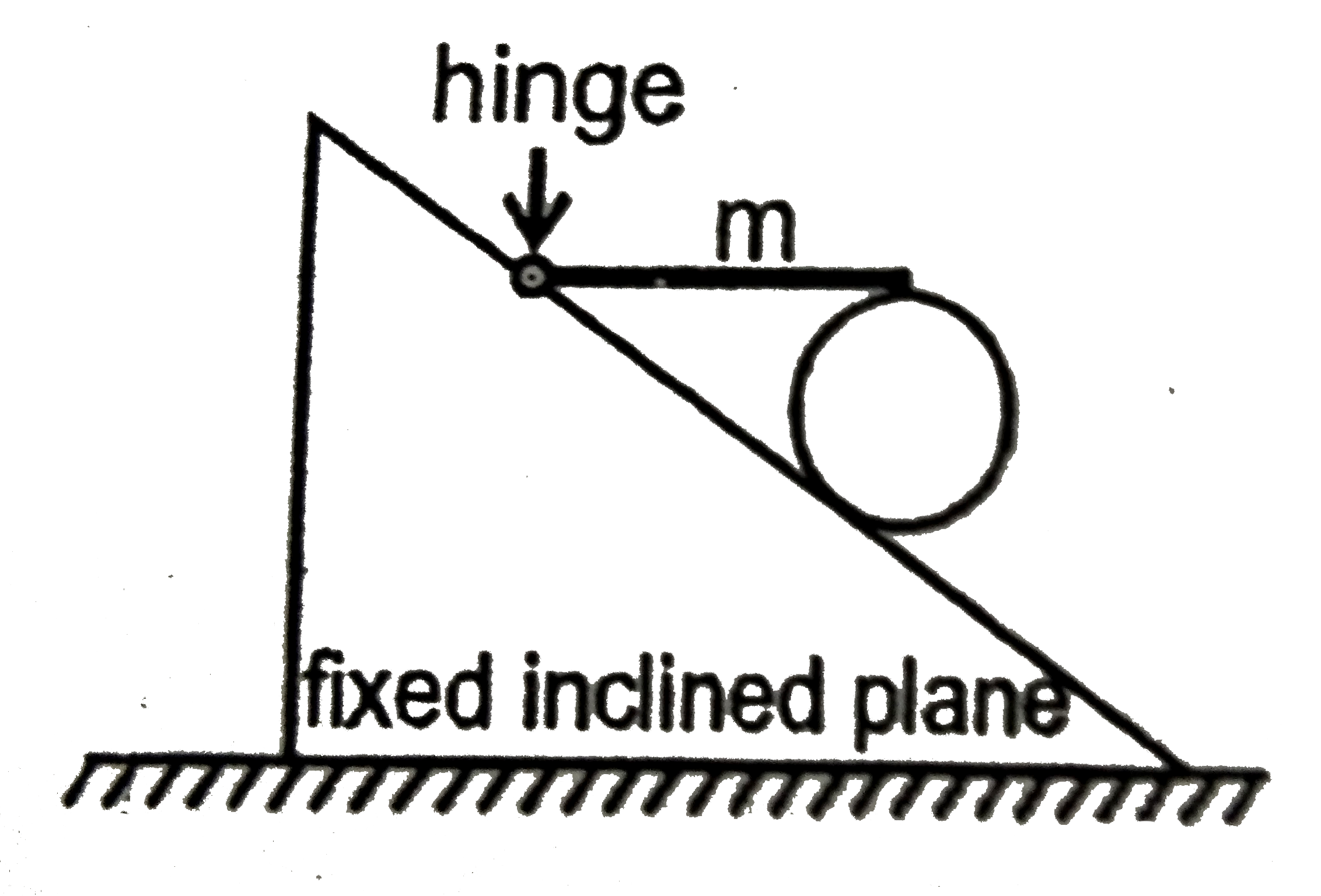
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
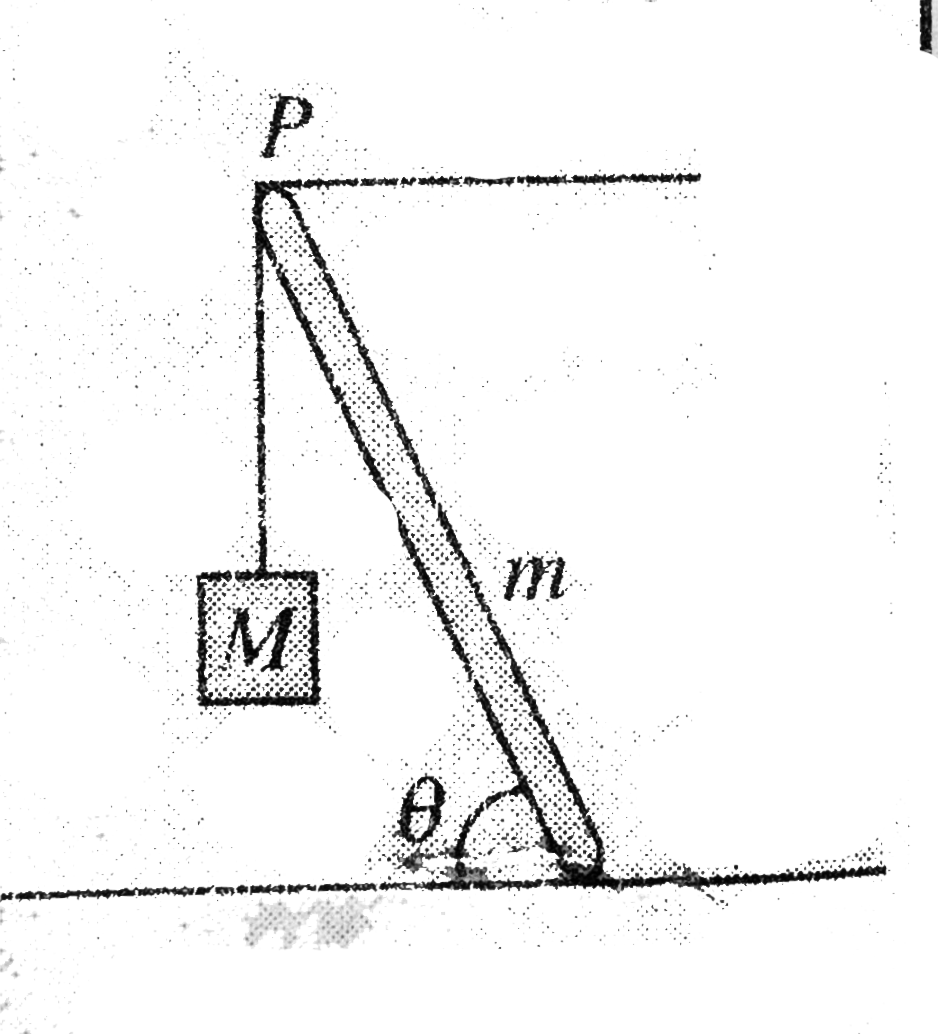 .
.
View SolutionDetermine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary, given that the coefficient of static friction between the box and truck's floor is 0.2.
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View Solution
