A uniform cylinder of radius r and mass m can rotate freely about a fixed horizontal axis. A thin cord of length l and mass m0 is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length x of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.

Figure shows the free body diagram of the two bodies. Viz., cylinder and overhnging portion of the cord.
If α is the angular acceleration of the cylinder then from τ=Iα.
we have Tr=[mr22+m0−m0l(l−x)r2]α
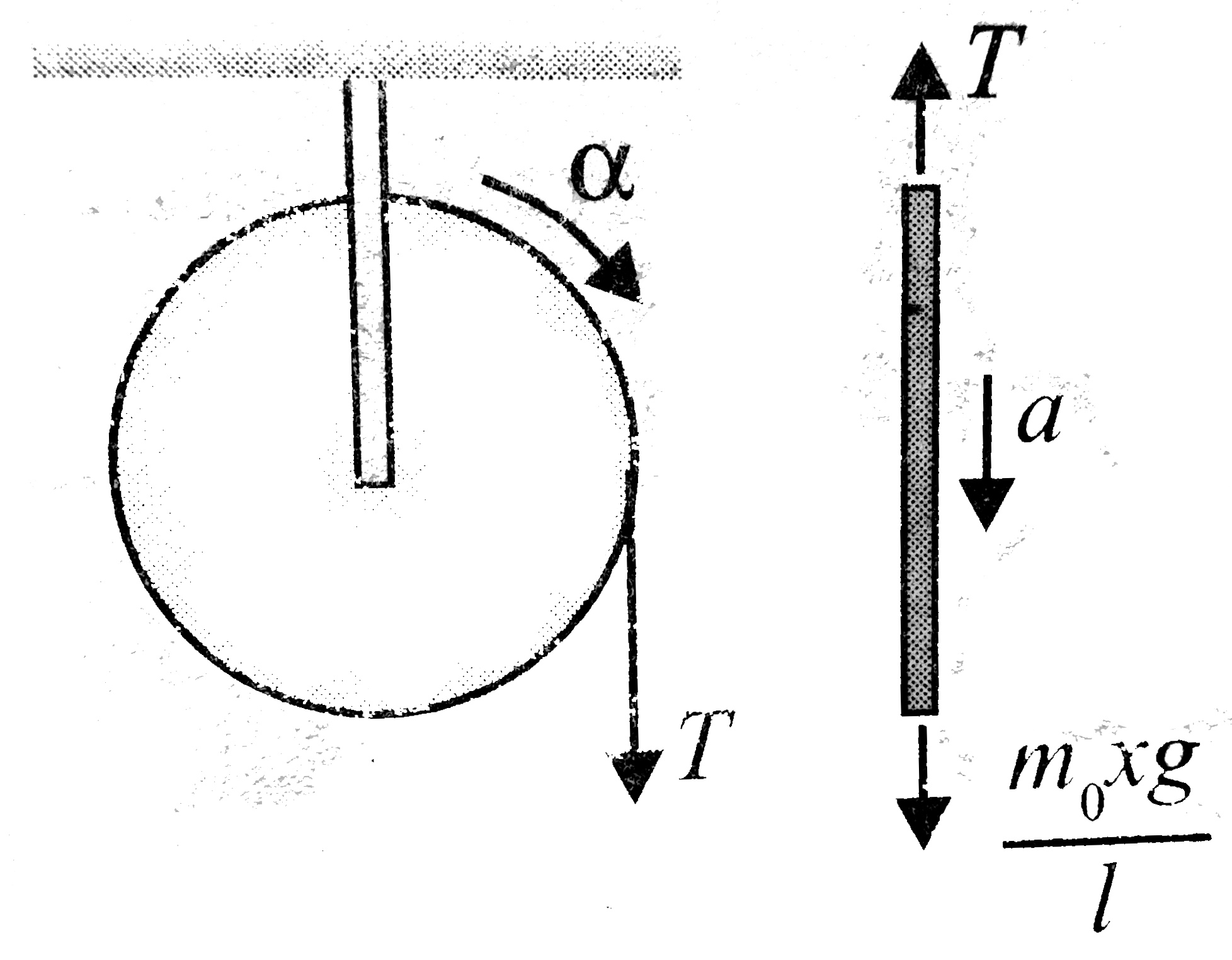
T=[m2+m0−m0xl]rα....i
If a be the acceleration of the hanging part, the from F=ma.
m0xgl−T=m0xla=m0xl(αr)..........ii
[Linear acceleration of the rim of the cylinder is same as that of the cord]
Adding eqn i and ii we get
m0xlg=α[m2+m0]r⇒α=m0xgrl[m2+m0]
Alternate method: Taking the cylinder and the cord as a single system moving in a gravitational, field, its total energy (mechanical) should remain constant
Assuming the level of the cylinder's centre as datum or refeence level , we have dEdt=0
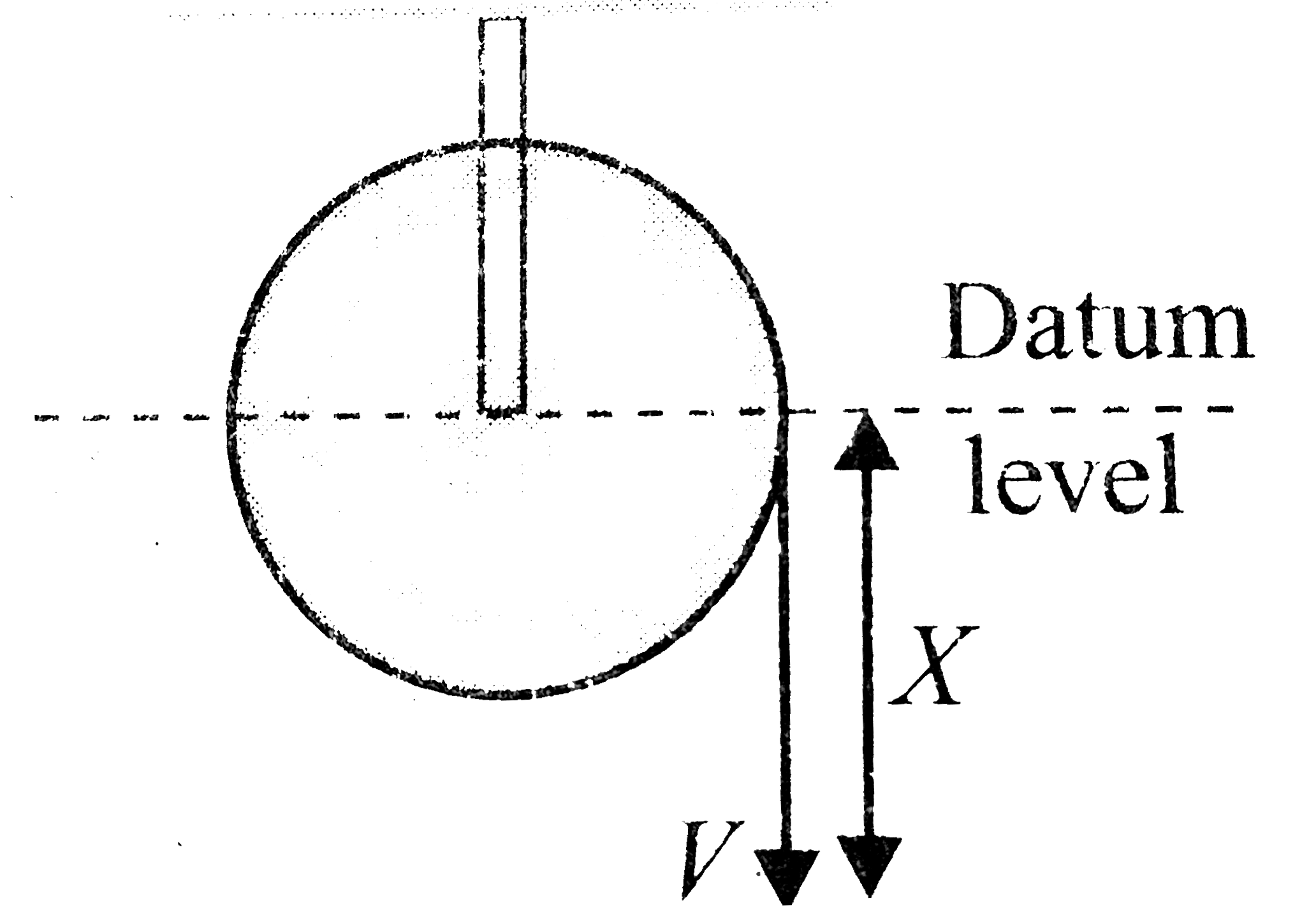
i.e., ddt[12(mr22)(vr)2+12m0v2−m0x1g(x2)]=0
[Here v is the speed of the hanging part]
⇒(m2+m0)2v(dvdt)−m0g1(2xdxdt)=0
⇒(m0+m2)dvdt=m0gx1⇒dvdt=m0gxl(m2+m0)
Therefore, the angular acceleration of the cylinder
=αr=m0gxrl(mm0)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.217videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
 View Solution
View SolutionA rope is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ?
View SolutionA rope is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ?
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
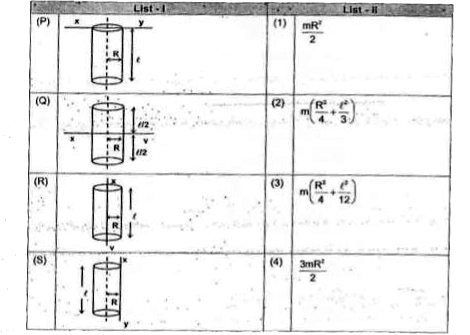 View Solution
View SolutionFigure shows a solid uniform cylinder of radius R and mass M, which is free to rotate about a fixed horizontal axis O and passes through centre of the cylinder. One end of an ideal spring of force constant k is fixed and the other end is higed to the cylinder at A. Distance OA is equal to R2. An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass M and having cross sectional area A is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density ρ.
If in equilibrium, spring is horizontal and line OA is vertical, calculate frequency of small oscillations of the system.
 View Solution
View SolutionA rectangular sheat of paper 44cm x 18cm is rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View SolutionA uniform solid. cylinder A of mass can freely rotate about a horizontal axis fixed to a mount of mass m2. A constant horizontal force F is applied to the end K of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find the acceleration of the point K.
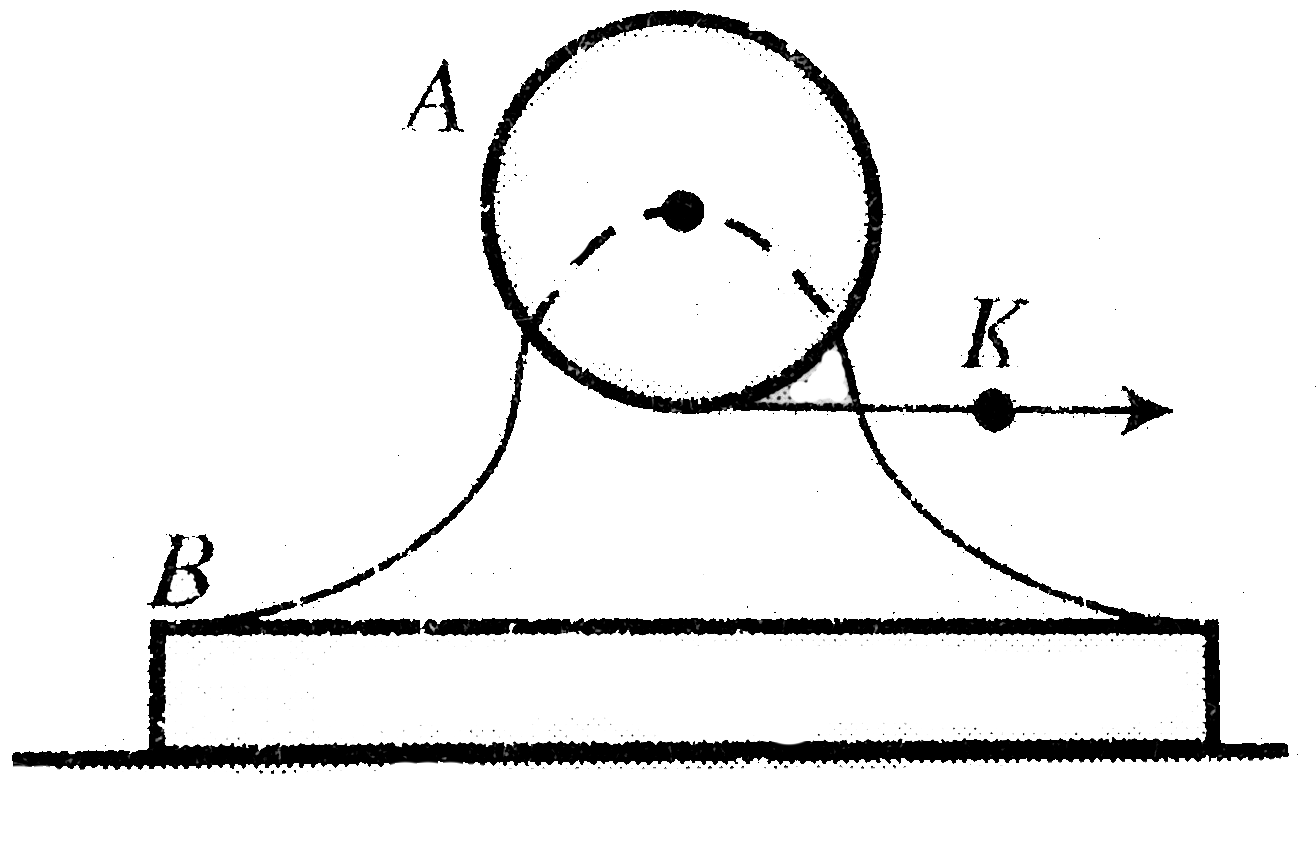 View Solution
View Solution
