A horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A ring having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
some friction exists between the disc and the ring
the angular momentum of the 'disc plus ring' is conserved
the final common angular velocity is (23)rd of the initial angular velocity of the disc
(23)rd of the initial kinetic energy changes to heat
The correct Answer is:A, B, D
Let ω1= the initial angular velocity of the disc ω2= the final common angular velocity of the disc and the ring.
For the disc
I1=12mr2
For the ring
I2=mr2
By coservation of angular momentum,
L=I1ω1=(I1+I2)ω2
ω2=I1ω1I1+I2=ω13
Initial kinetic energy =E1=12I1ω21
Final kinetic energy =E1=12(I1+I2)ω22
Heat produced = loss in KE
Ratio of heat produced to initial kinetic energy =E1−E2E1=23
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddenly attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View Solution
Knowledge Check
When a disc rotates with uniform angular velocity, which of the following is not true ?
Aa. The sense of rotation remains same.Bb. The orientation of the axis of rotation remains same.Cc. The speed of rotation is non-zero and remains same.Dd. The angular acceleration is non-zero and remains same.
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA smoothh disc is rotating with uniform angular speed ω about a fixed vertical axis passing through its centre and normal to its plane as shown. A small block of mass m is gently placed at the periphery of the disc. Then (pickup the correct alternative or alternatives)
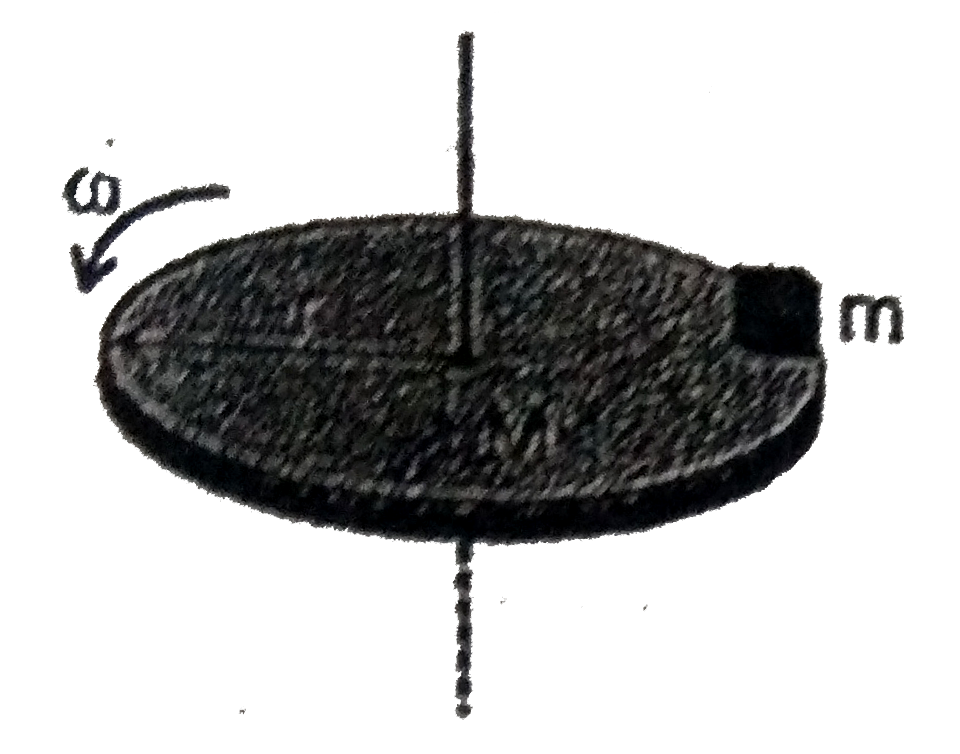
View SolutionA disc has mass 'M" and radius 'R'. How much tangential force should be applied to the rim of the disc so as to rotate with angular velocity ω in time 't'?
View SolutionWhen a disc rotates with uniform angular velocity, which of the following is not true ?
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is
View SolutionA metal disc of radius a rotates with a constant angular velocity ω about its axis. The potential difference between the center and the rim of the disc is (m = mass of electron, e = charge on electro)
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system is
View Solution
