Question

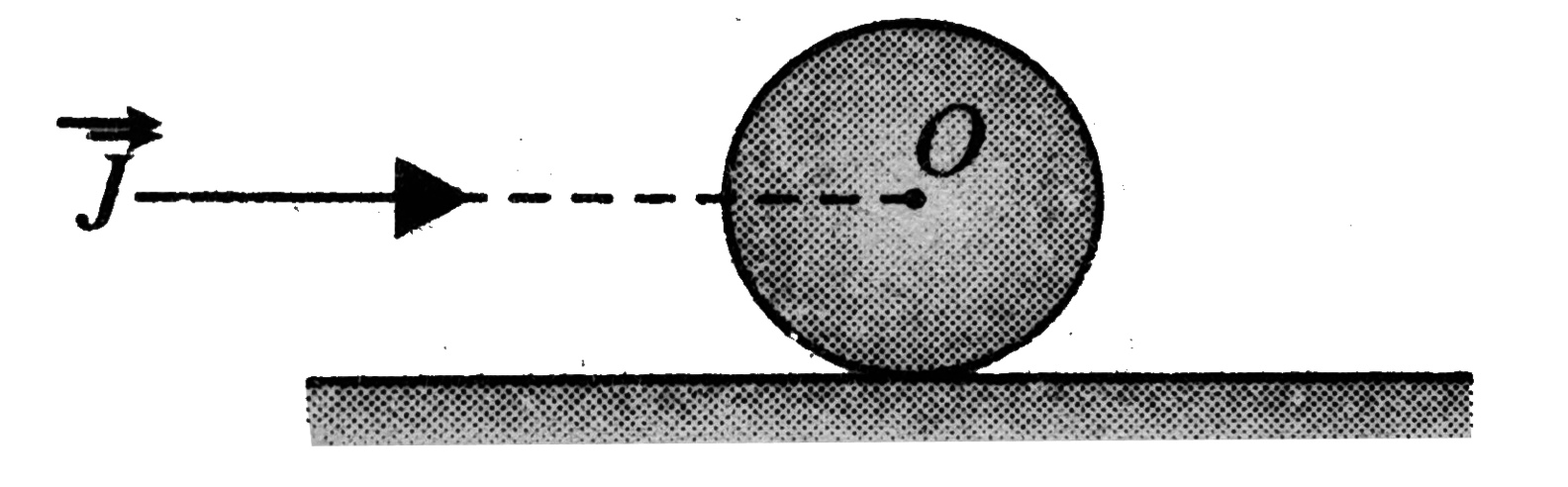
An impulse J is applied on a ring of mass m along a line passing through its centre O. the ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without spilling is

Options

A. `J//m`
B. `J//2m`
C. `J//4m`
D. `J//3m`

Answer

B

Explanation

Let `v` be the velocit of `COM` of ring just after the impule is applied and `v'` its velocity when pure rolling starts. Angular velocity `omega` of the ring at this instant will be `omega=(v^('))/r`.

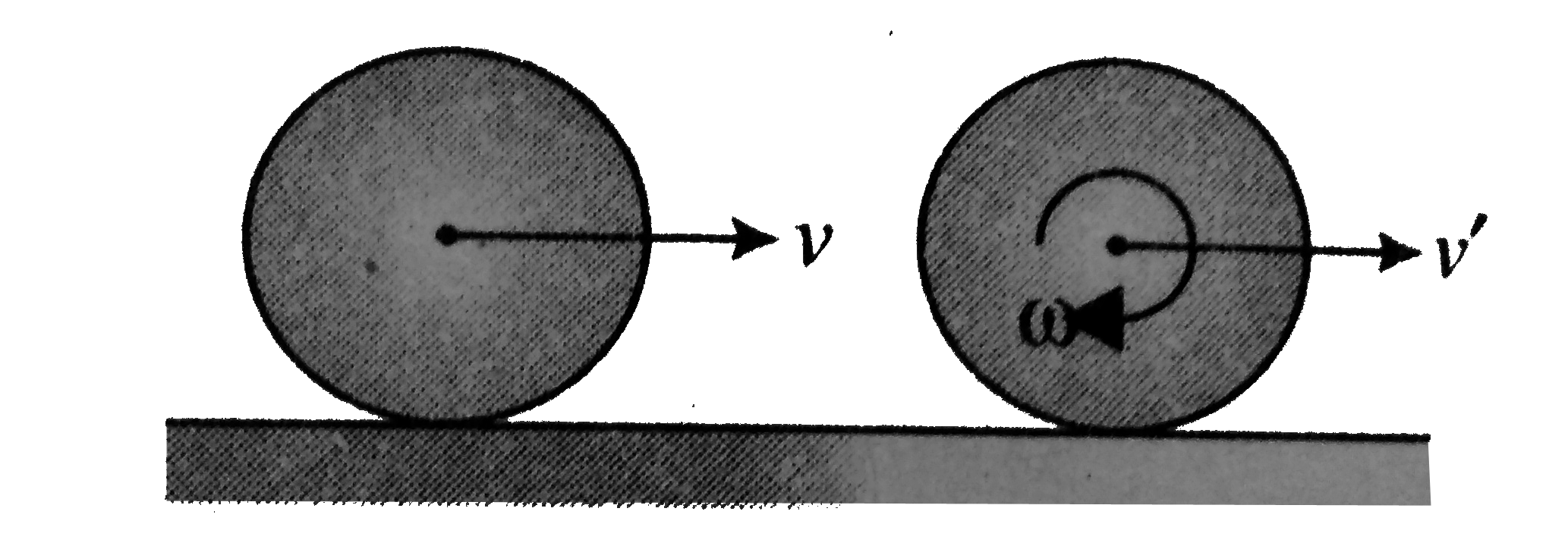
From impulse =change in linear momentum, we have
`J=mv`
or `v=J/m`.....i
Between the two positions shown in figure, force of friction on the ring acts backwards. So angular momentum of the ring about bottommost point will remain conserved
`:. L_(i)=L_(f)`
or `mr=mv'r+Iomega`
`mv'r+(mr^(2))((v^('))/r)=2mg'r`
`v'=v/2 =J/(2m)` (from equation)