There are four solid balls with their centres at the four corners of a square of side a. the mass of each sphere is m and radius is r. Find the moment of inertia of the system about one of the sides of the square
a. Moment of inertia of the arrangement about the diagonal AC:
The moment of inertia of each of spheres A and C about their common diameter AC=(25)ma2. The moment of inerta of each of spheres B and D about an axis passing through their centres and parallel to AC is (25)ma2. The distance between the axis and AC is b√2, b being side of the square. therefore the moment of inertia of each spheres B and D about AC by the theorem of parallel axis is
25ma2+m(b√2)2=25ma2−mb22
Therefore, the moment of inertias of all the four spheres about diagonal AC is
I=2(25ma2)+2[25ma2+mb22]
b. The moment of inertia of each of spheres A and D about side AD is (25)ma2.
The moment of inertia of each of sphere B and C about AD is (25)ma2+mb2.
Therefore the moment of inertia of the whole arrangement about side AD is
2[25ma2+(25ma2+mb2)]=2m5[42+5b2]
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Solved Examples
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Four spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
View SolutionFour spheres A, B, C, D, each of mass m and diameter 2 a are placed with their centres at die four corners of a square of side b. What is the moment of inertia of the system about any side of the square ?
View SolutionFour solid sphereas each of diameter √5cm and mass 0.5kg are placed with their centres at the corners of a square of side 4cm. The moment of inertia of the system about the diagonal of the square is N×10−4kg−m2, the N is -
View SolutionFour thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionA square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)
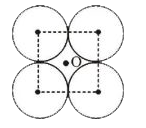
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)

View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionFour particles each of mass 'm' are kept at the four corners of a square of edge 'a'. Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the center of the square.
View Solution
