A block hangs freely from the end of a spring. A boy then slowly pushes the block upwards so that the spring becomes strain free. The gain in gravitational potential energy of the block during this process is not equal to
(a) The work done by the boy against the gravitational force acting on the block
(b) The loss of energy stored in the spring minus the work done by the tension in the spring
(c) The work done on the block by the boy plus the loss of energy stored in the spring
(d) The work done on the block by the boy minus the work done by the tension in the spring plus the loss of energy stored in the spring
(e) The work done on the block by the boy minus the work done by the tension in the spring
The correct Answer is:A, B, D
To solve the problem step by step, we need to analyze the situation where a block is hanging from a spring and is pushed upwards until the spring is strain-free. We want to determine which of the given options does not equal the gain in gravitational potential energy of the block during this process.
Step 1: Understand the System
- A block of mass m is hanging from a spring. The weight of the block is mg, where g is the acceleration due to gravity.
- When the block is hanging freely, it stretches the spring by an amount x. The spring force is given by Hooke's Law as Fs=kx, where k is the spring constant.
Step 2: Determine the Relationship Between Forces
- At equilibrium (when the block is hanging freely), the gravitational force equals the spring force:
mg=kx
From this, we can express x:
x=mgk
Step 3: Calculate the Gain in Gravitational Potential Energy
- The gain in gravitational potential energy (ΔU) when the block is pushed upwards by the distance x is:
ΔU=mgx
- Substituting x from the previous step:
ΔU=mg(mgk)=m2g2k
Step 4: Analyze Each Option
Now we will analyze each option to see which one does not equal the gain in gravitational potential energy.
Option A: Work done by the boy against the gravitational force acting on the block.
- This is equal to the gain in potential energy, so it's equal to ΔU.
Option B: Loss of energy stored in the spring minus the work done by the tension in the spring.
- The loss of energy stored in the spring is 12kx2 and the work done by the tension is also 12kx2. Thus, this results in 0, which is not equal to ΔU.
Option C: Work done on the block by the coil plus loss of energy stored in the spring.
- This results in ΔU, so it is equal.
Option D: Work done on the block by the boy minus work done by the tension in the spring plus the loss of energy stored in the spring.
- This also results in ΔU, so it is equal.
Option E: Work done on the block by the boy minus the work done by the tension in the spring.
- This results in ΔU, so it is equal.
Conclusion
The only option that does not equal the gain in gravitational potential energy is Option B.
- A block of mass m is hanging from a spring. The weight of the block is mg, where g is the acceleration due to gravity.
- When the block is hanging freely, it stretches the spring by an amount x. The spring force is given by Hooke's Law as Fs=kx, where k is the spring constant.
- At equilibrium (when the block is hanging freely), the gravitational force equals the spring force:
mg=kx
From this, we can express x:
x=mgk
- The gain in gravitational potential energy (ΔU) when the block is pushed upwards by the distance x is:
ΔU=mgx
- Substituting x from the previous step:
ΔU=mg(mgk)=m2g2k
Now we will analyze each option to see which one does not equal the gain in gravitational potential energy.
- This is equal to the gain in potential energy, so it's equal to ΔU.
- The loss of energy stored in the spring is 12kx2 and the work done by the tension is also 12kx2. Thus, this results in 0, which is not equal to ΔU.
- This results in ΔU, so it is equal.
- This also results in ΔU, so it is equal.
- This results in ΔU, so it is equal.
The only option that does not equal the gain in gravitational potential energy is Option B.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
One end of an unstretched vertical spring is attached to the ceiling and an object attached to the other end is slowly lowered to its equilibrium position. If S is the gain in spring energy and G is the loss in gravitational potential energy in the process, then
View SolutionTwo blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
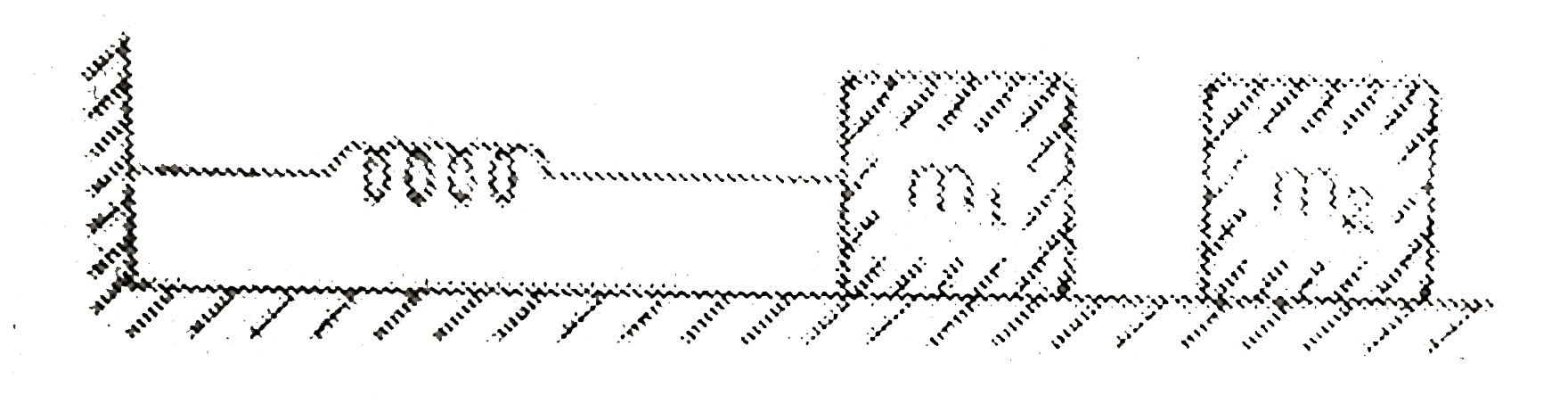
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionTwo blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
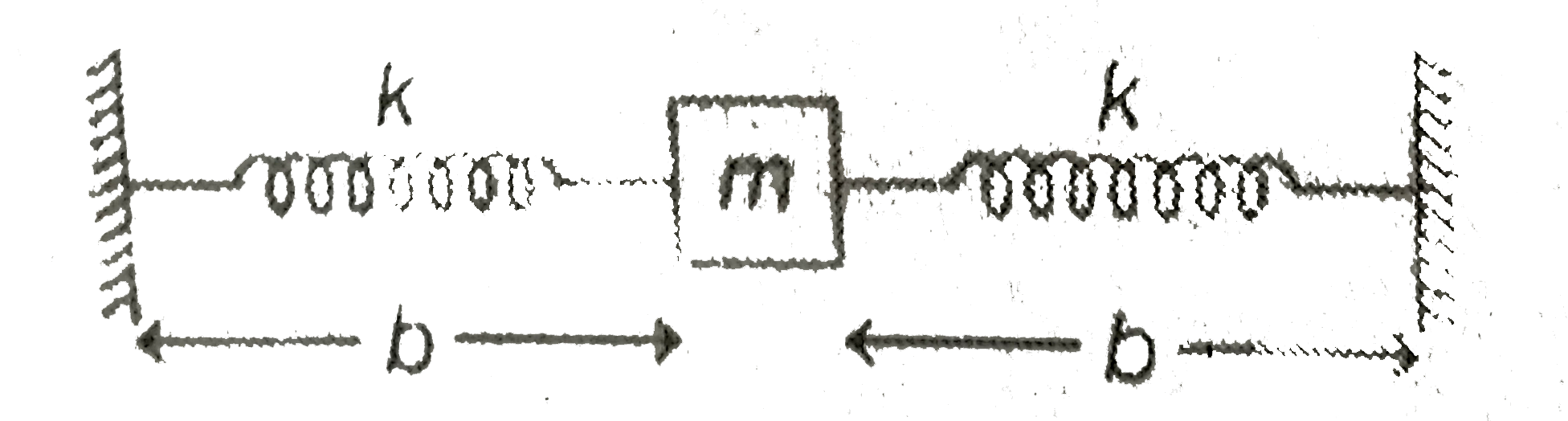
View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
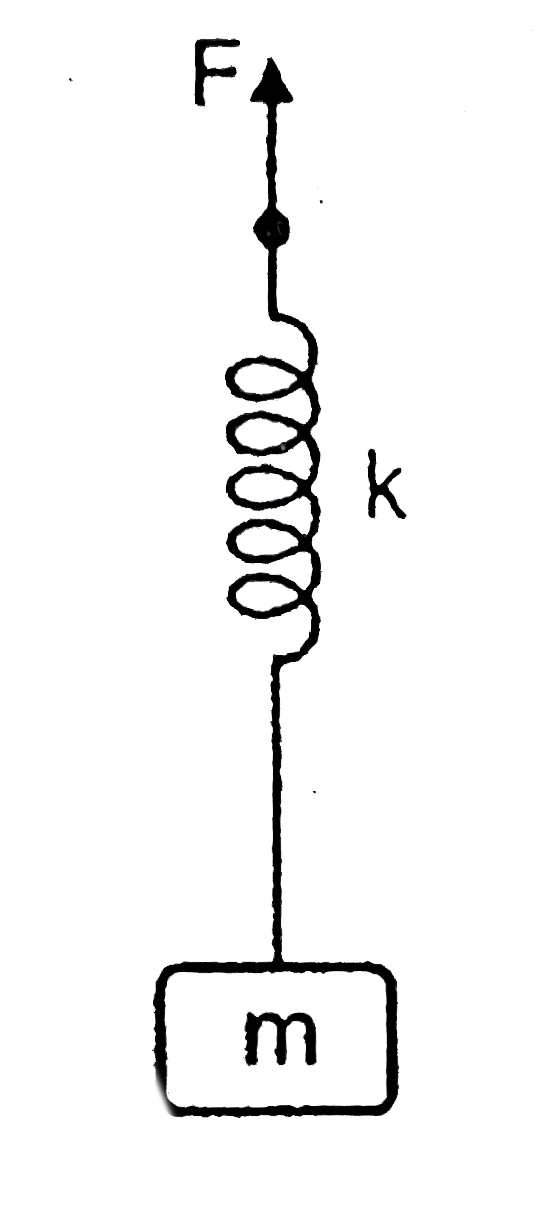
View SolutionA block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
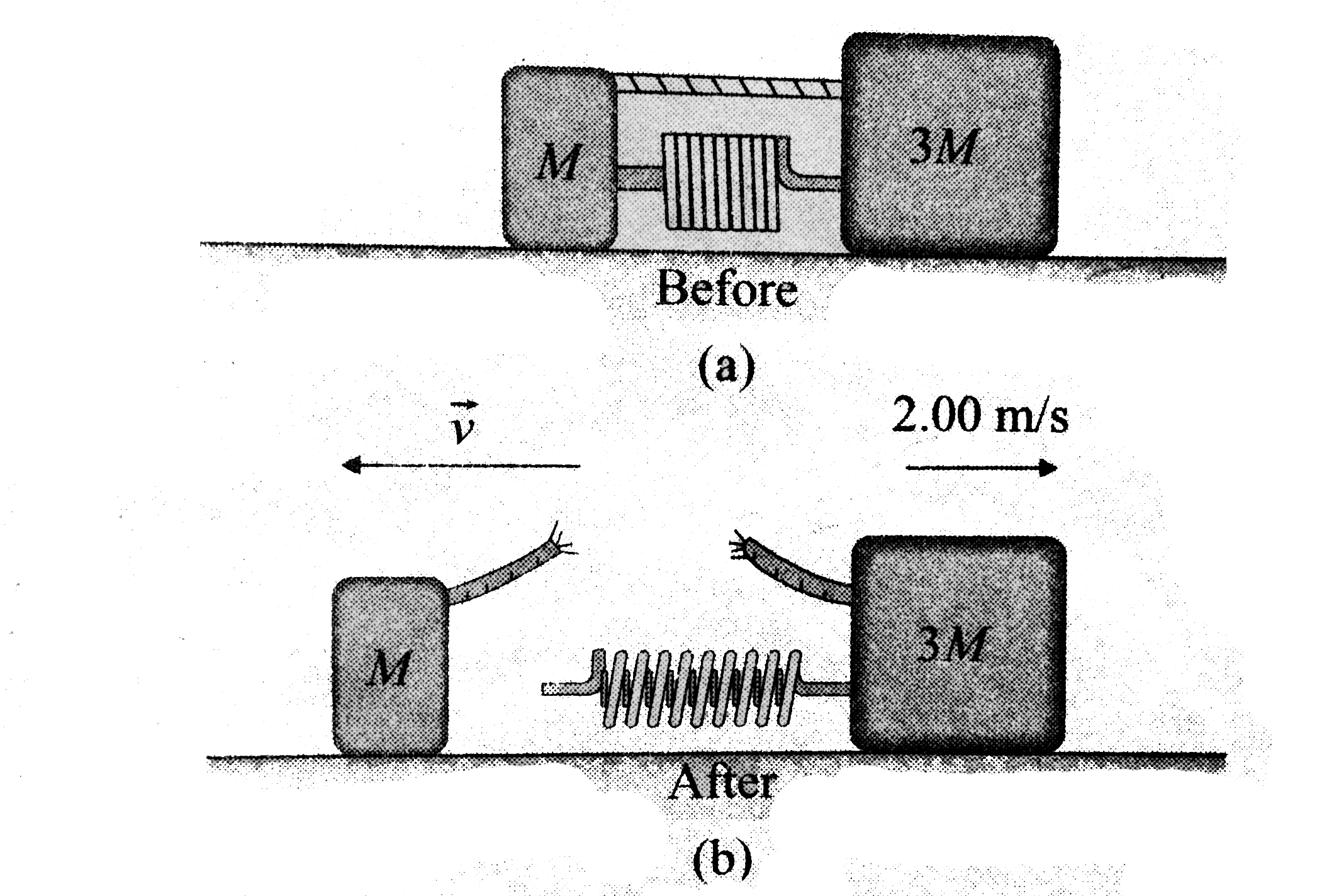
View SolutionTwo blocks of masses M and 3M are placed on a horizontal, frictionless surface. A light spring is attached to one of them and the blocks are pushed together with the spring between them. A cord initially holding the blocks together is burned, after that, the block of mass 3M moves to the right with a speed of 2.00m/s. (a) What is the velocity of the block of mass M. (b) Find the system's original elastic potential energy, taking M=0.350kg. (c) Is the original energy in the spring or in the cord? Explain your answer. (d) Is momentum of the system conserved in the bursting apart process? How can it be with large forces acting? How can it be with no motion beforehand and plenty of motion afterward?
View Solution
