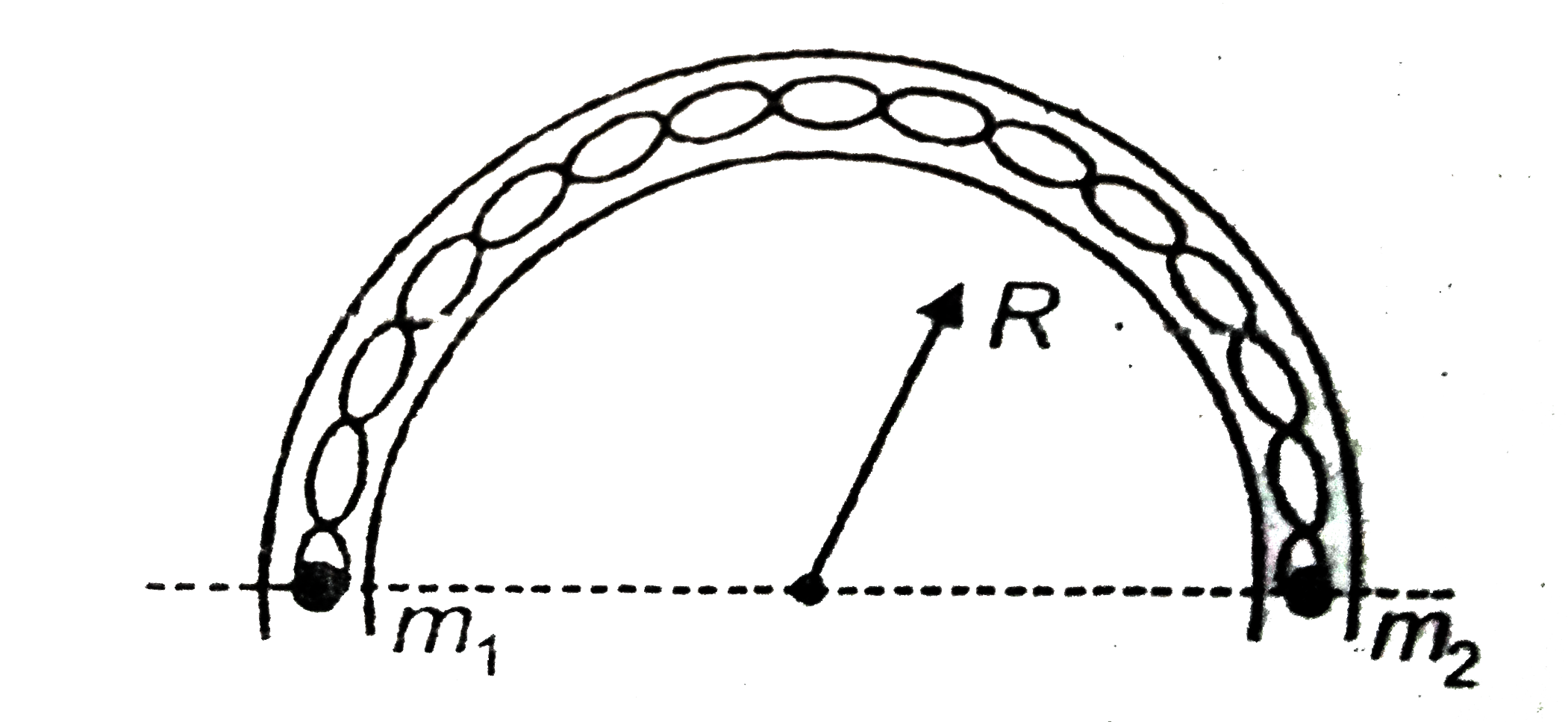
Two smooth balls of mass $m_{1}$ and $m_{2}$ connected by a light inextensible string are at the opposite points of horizontal diameter of a smooth semi cylindrical surface of radius R. If $m_{1}$ is released, find its speed at any angular distance $θ$ moved by $m_{2}$ .

Video Solution

Text Solution

Verified by Experts

Let the ball $m_{2}$ moves through an angle $θ$ . The mass $m$ will fall through a distance $h_{1} = R θ$ .
The ball $m_{2}$ rises through a height $h_{2}$ as,
$h_{2} = R sin θ$ .

The change in gravitational potential energy of $m_{1}$ is
$Δ U_{1} = - m_{1} g h_{1} = - m_{1} g R θ$
(since $m_{1}$ loses its potential energy as it falls down).
The change in gravitational potential energy of $m_{2}$ is
$Δ U_{2} = m_{2} g h_{2} = m_{2} g R sin θ$
(since $m_{2}$ gains potential energy as it rises up)
$\Rightarrow$ The total change in gravitational potential energy=
$Δ U = Δ U_{1} + Δ U_{2}$ (i)
$\Rightarrow Δ U = - m_{1} g R θ + m_{2} g R sin θ = g R (m_{2} sin θ - m_{1} θ)$ .
The change in KE of the system $(m_{1} + m_{2})$ ,
$Δ K = \frac{1}{2} m_{1} v^{2} + \frac{1}{2} m_{2} v^{2} = \frac{(m_{1} + m_{2}) v^{2}}{2}$ (ii)
where v=speed of $m_{1}$ and $m_{2}$ at the positions as shown in the figure.
From the principle of conservation of energy we obtain,
$Δ K + Δ U = 0$ (iii)
Using (i), (ii) and (iii), we obtain,
$\frac{1}{2} (m_{1} + m_{2}) v^{2} - g R (m_{1} θ - m_{2} sin θ) = 0$
$\Rightarrow v = \sqrt{\frac{2 g R (m_{1} θ - m_{2} sin θ)}{(m_{1} + m_{2})}}$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-WORK, POWER & ENERGY-Exercise 8.3

Home
Ask Doubt
Profile