Two identical balls each of mass m interconnected by a small light inextensible string are kept on a smooth horizontal surface. One of the balls is pushed towards the other with a speed v0 find the loss of K.E. of the ball. What will be the final velocities of the balls ? (e=1).

We know that, when two identical bodies collide elastically, they transfer their momenta. That means, Just after collision the stationary ball starts moving with a speed v0 and the first ball will be stationary. The second ball will continue moving with speed, say, v. Since no external force is acting on the system of the balls and string (tension in the string is internal force), the system conserves its linear momentum. Conserving the momentum of the system just before and after the string taul obtain.
mv0=mv+mv
⇒v=v02
(a) Now the loss in K.E. of the ball
ΔKE=12mv2+12mv2−12mv20
Putting v=v02, value of ΔKE can be found.
Similar Questions
Two identical small balls, each of mass m, are connected by a massless and inextensible string of length l and placed on a smooth horizontal xy plane. An external agent pulling the string from its mid-point along y-axis with velocity v0 as shown in Fig. When the separation between the two balls reduces to l/2 then the speed of each ball will be
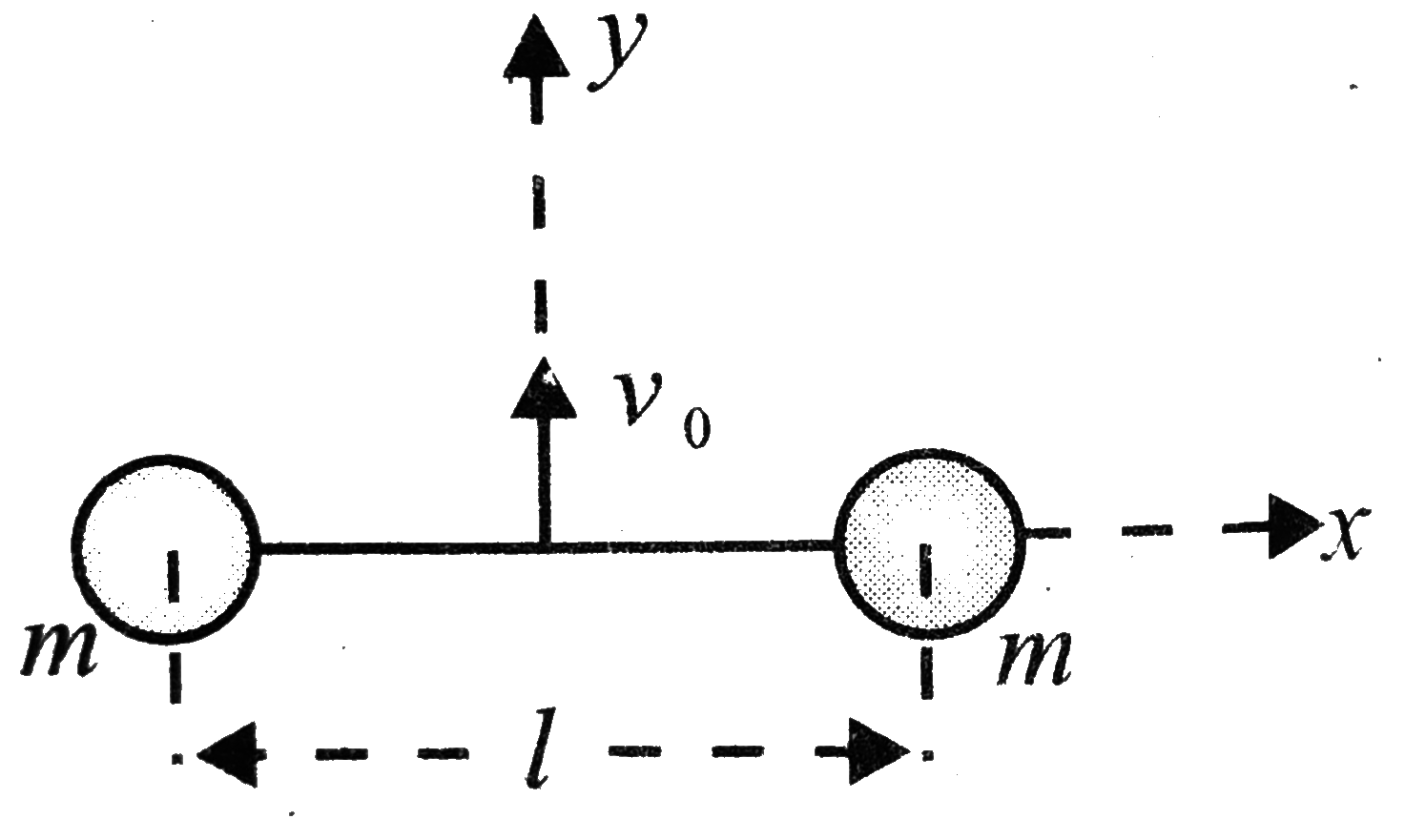
View SolutionTwo identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

What is the final loss in kinetic energy of the balls?
View SolutionTwo smooth balls of mass m1 and m2 connected by a light inextensible string are at the opposite points of horizontal diameter of a smooth semi cylindrical surface of radius R. If m1 is released, find its speed at any angular distance θ moved by m2.

View SolutionThree identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. Length of each string is l.
At moment t=0, ball B is imparted a velocity v0 perpendicular to the strings and then the system is left on its own.

If collision between the balls is completely inelastic, then
View SolutionThree identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. Length of each string is l.
At moment t=0, ball B is imparted a velocity v0 perpendicular to the strings and then the system is left on its own.

Calculate the velocity of A at the above given instant.
View SolutionTwo identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

After the first collision, what is the total loss in kinetic energy of the balls?
View SolutionTwo balls of masses m1=5kg,m2=10kg are connected by a light inextensible string. A horizontal force F = 15 N is acting on the ball m2 along the line joining two balls as shown. What is the (a) acceleration of the balls (b) tension in the string?

View SolutionThree identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table. Length of each string is l.
At moment t=0, ball B is imparted a velocity v0 perpendicular to the strings and then the system is left on its own.

Calculate the velocity of B just before A collides with ball C.
View Solution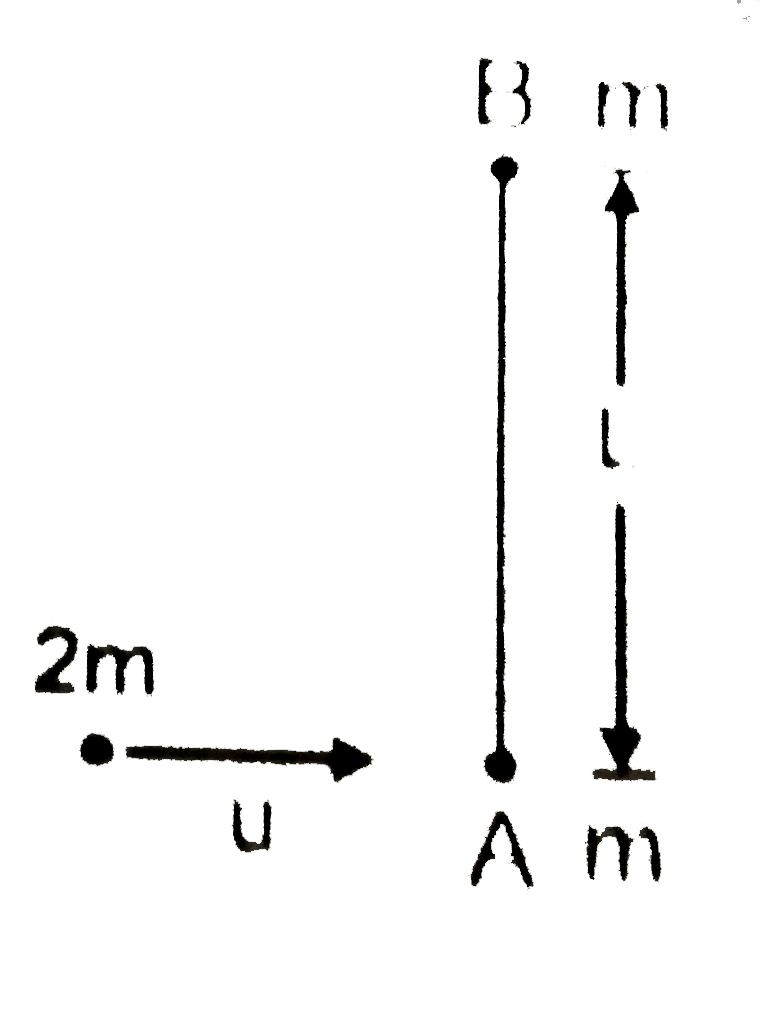
Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rof of length L. they are placed on a frictionless horizontal surface another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown int he figure. if the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be
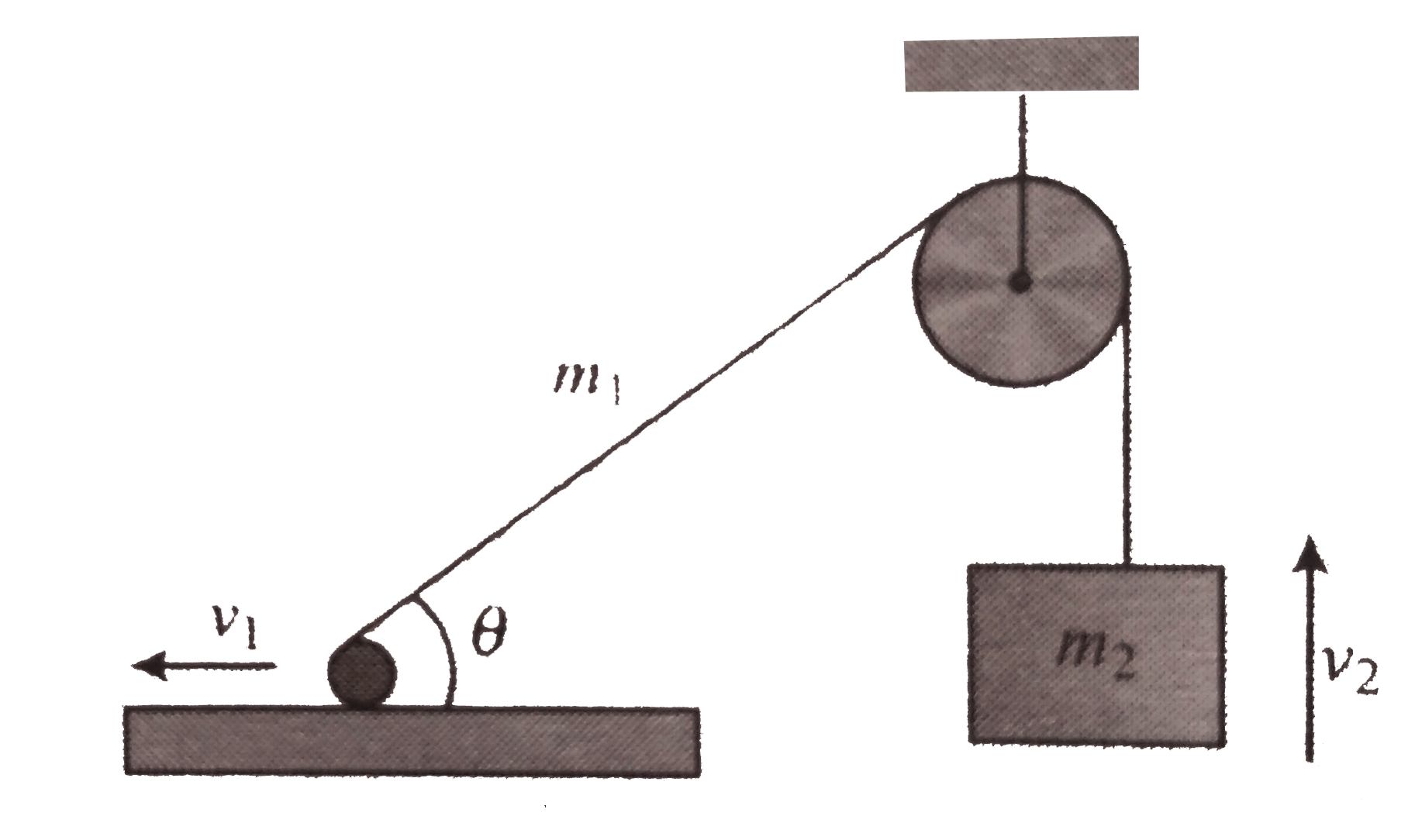
View SolutionIn fig. a ball of mass m1 and a block of mass m2 are joined together with an inextensible string. The ball can slide on a smooth horizontal surface. If v1 and v2 are the respective speeds of the ball and the block, then determine the constraint relation between the two.
View Solution