In figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
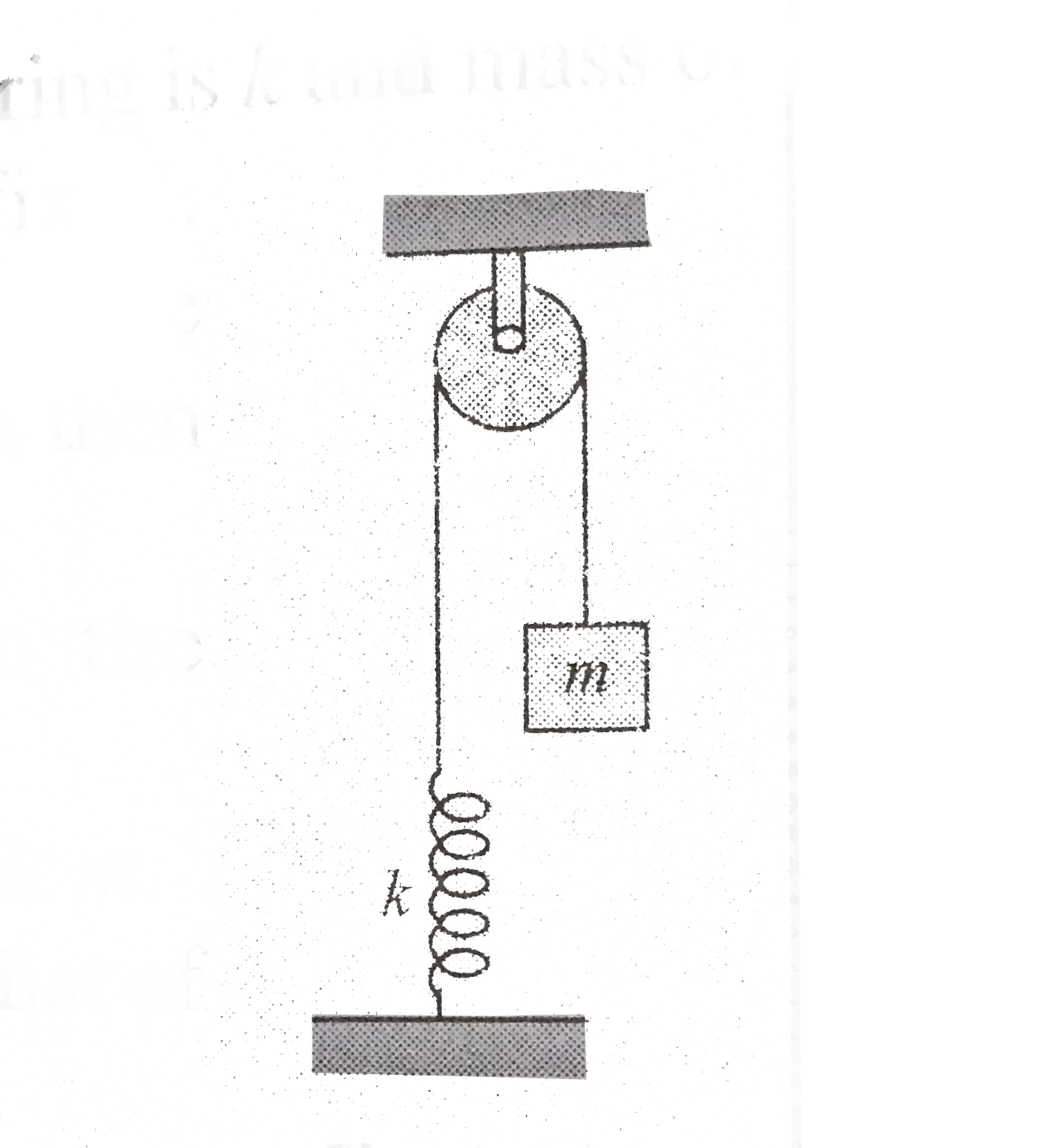
Let the maximum elongation in the spring be x, when the block is at position 2.
a. The displacement of the block m is also x.
From conservation of energy, ΔK=ΔU=0
=12kx2=mgx
⇒x=2mg/k
b. Let maximum velocity occur when block moves a distance x.
Using ΔK+ΔU=0
(12mv2−0)+(−mgx+12kx2)=0
or 12mv2=mgx−12kx2
Differeciating above equations w.r.t. x
12m⋅2v⋅dvdx=mg(dx)dt−12k2xdxdt
mv⋅dvdt=mgv−kxv
For maximum v, dvdx=0⇒x=mgk
So, mg(mgk)−12k(mgk)2=12mv2max
⇒vmax=(√mk)g
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.4
Explore 16 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.5
Explore 15 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.2
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionIn a vertical spring mass system, a block of mass m is initially at rest when there is no extension. Now if the mass is released suddenly, then the maximum elongation in the spring is
View SolutionInitially mass m is held such that spring is in relaxed condition. If mass m is suddenly released, maximum elongation in spring will be

View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
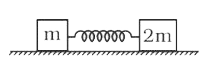
View SolutionA spring is connected between two blocks as shown in the diagram. Initially the blocks are held stationary and suddenly they are released. Find the ratio of maximum kinetic energy with spring compressed the block of mass m to that of mass 2m.
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension
 .
.
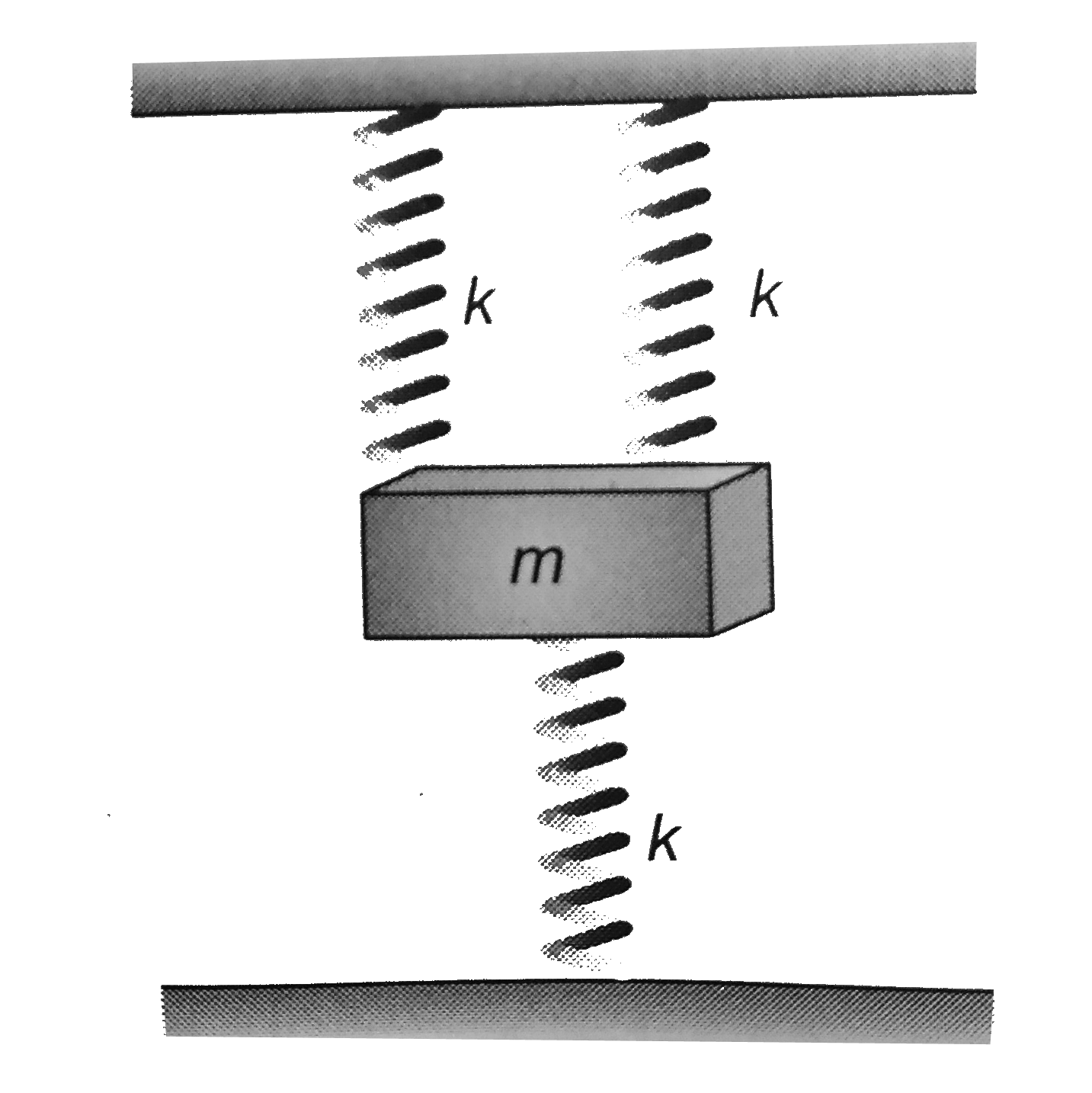
View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
View Solution

