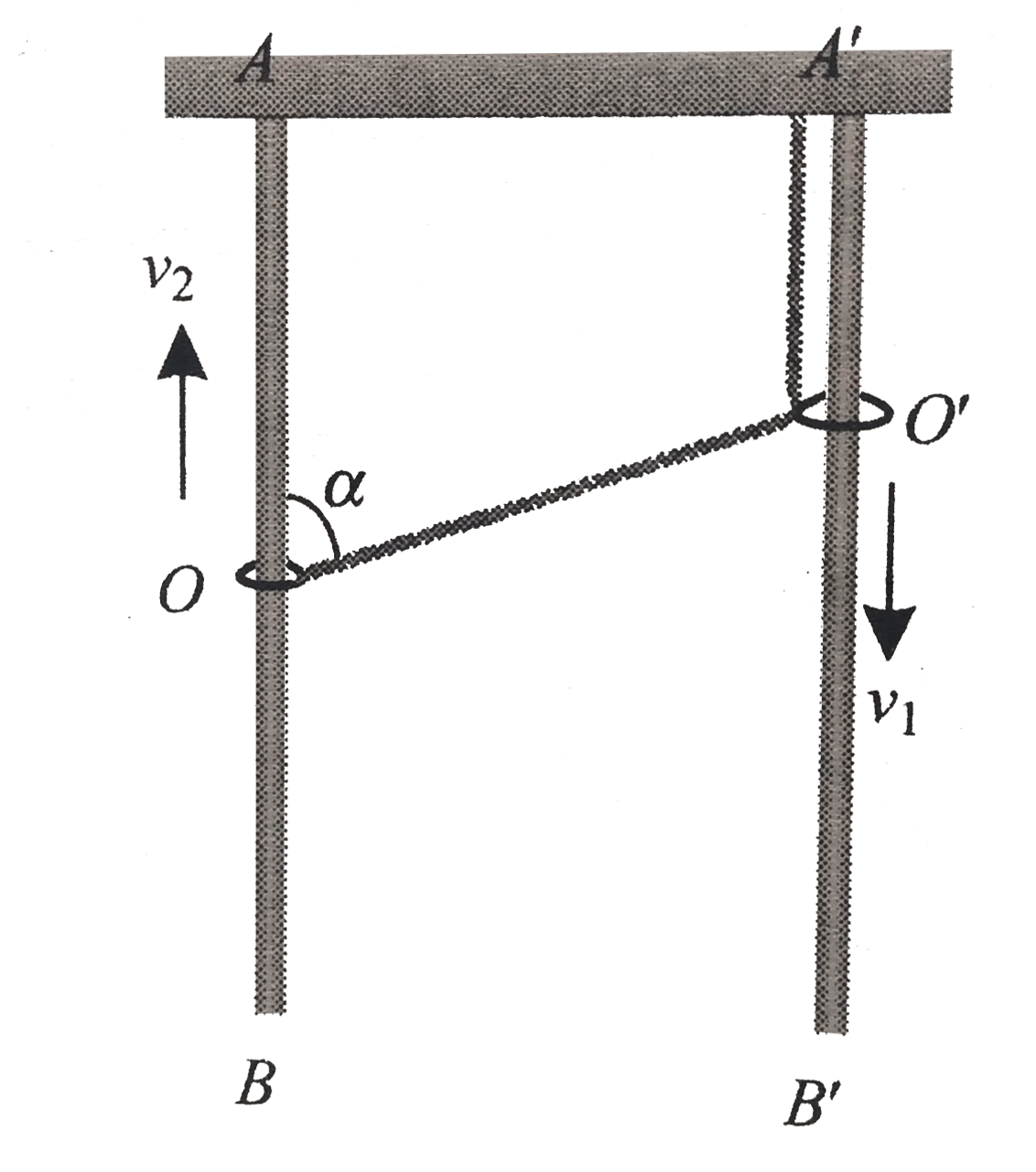
Two small rings O and O' are put on two vertical stationary rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O. Assuming that ring O' moves downwards at a constant velocity v1, then velocity v2 of the ring O, when ∠AOO'=α is
v1[2sin2α/2cosα]
v1[2sin2α/2sinα]
v1[3sin2α/2sinα]
None of these
The correct Answer is:A
v2cosα+v1cosα=v1⇒v2=v1[2sin2(α/2)cosα].
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
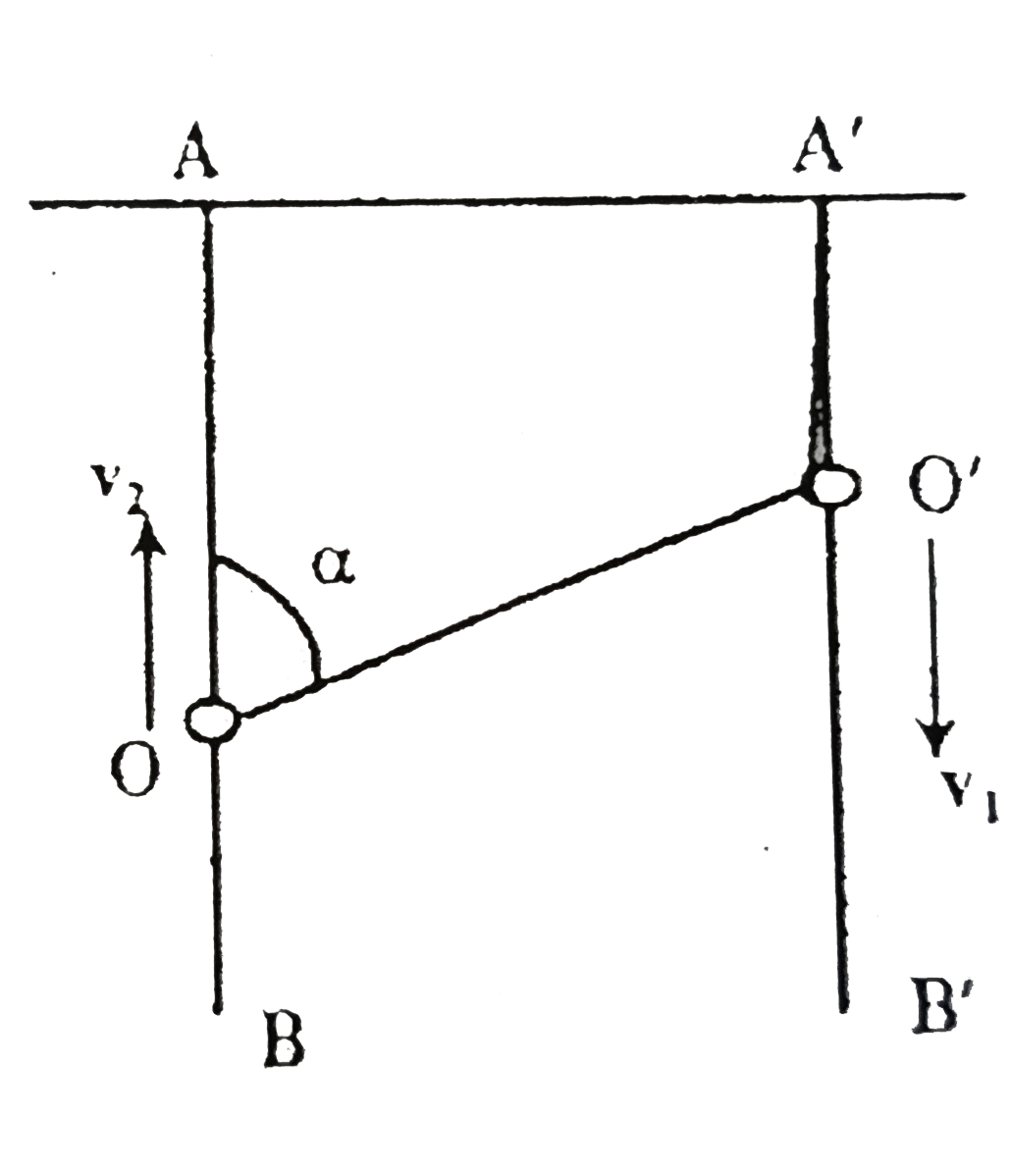
Two small rings O and O' are put on two vertical stationery rods AB and A'B', respectively. One end of an inextensible thread is tied at point A'. The thread passes through ring O' and its other end is tied to ring O.
Assuming that ring O' moves downwards at a constant velocity v1, determine the velocity v2 of the ring O, when ∠AOO'=α.
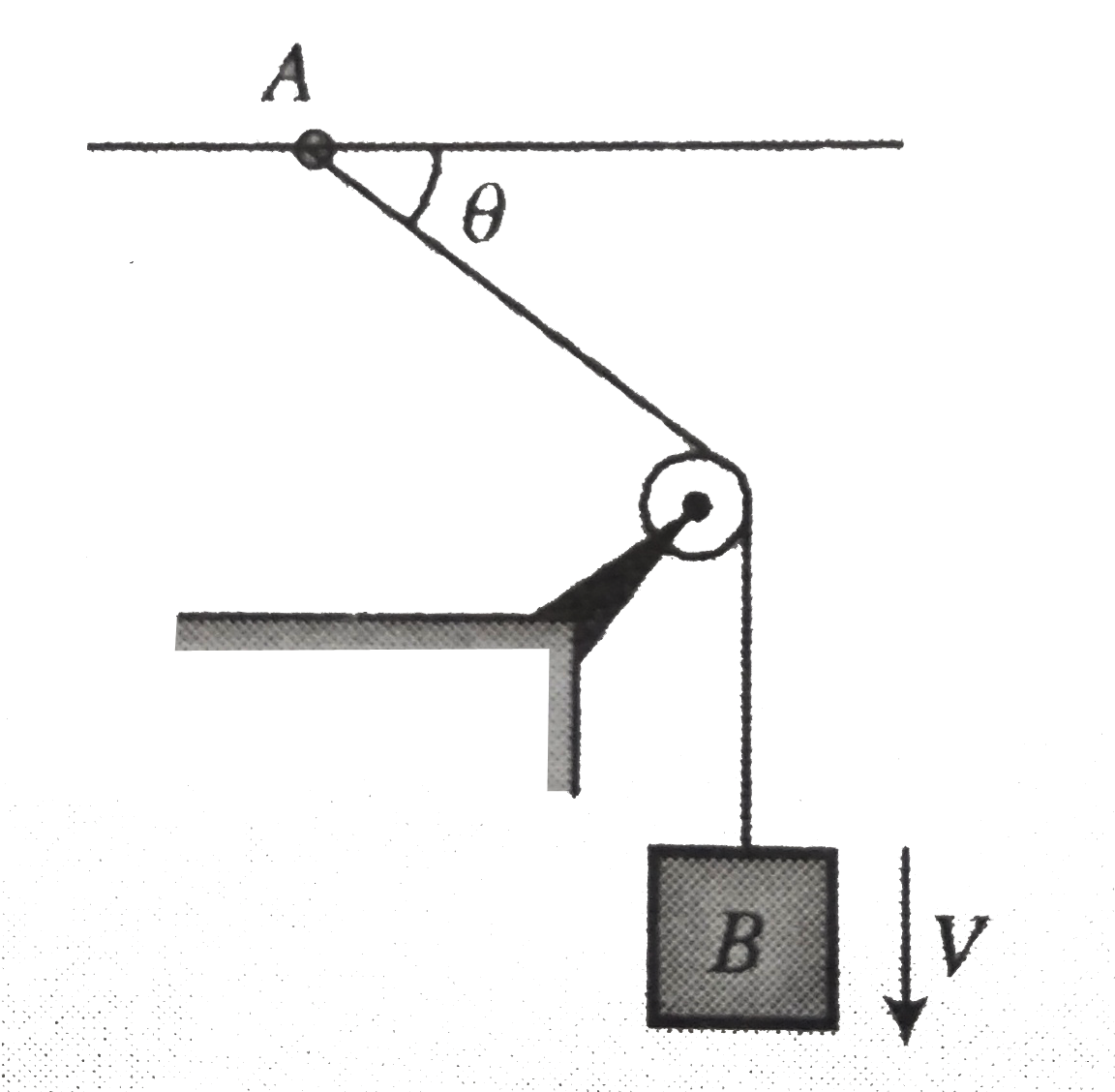
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
View SolutionThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. Then I1/I2 is
View SolutionA small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)
View SolutionIn Fig. a pulley is shown which is frictionless and a ring of mass m can slide on the string without any friction. One end of the string is attached to point B and to the other end, a block 'P' of mass m is attached. The whole system lies in vertical plane.
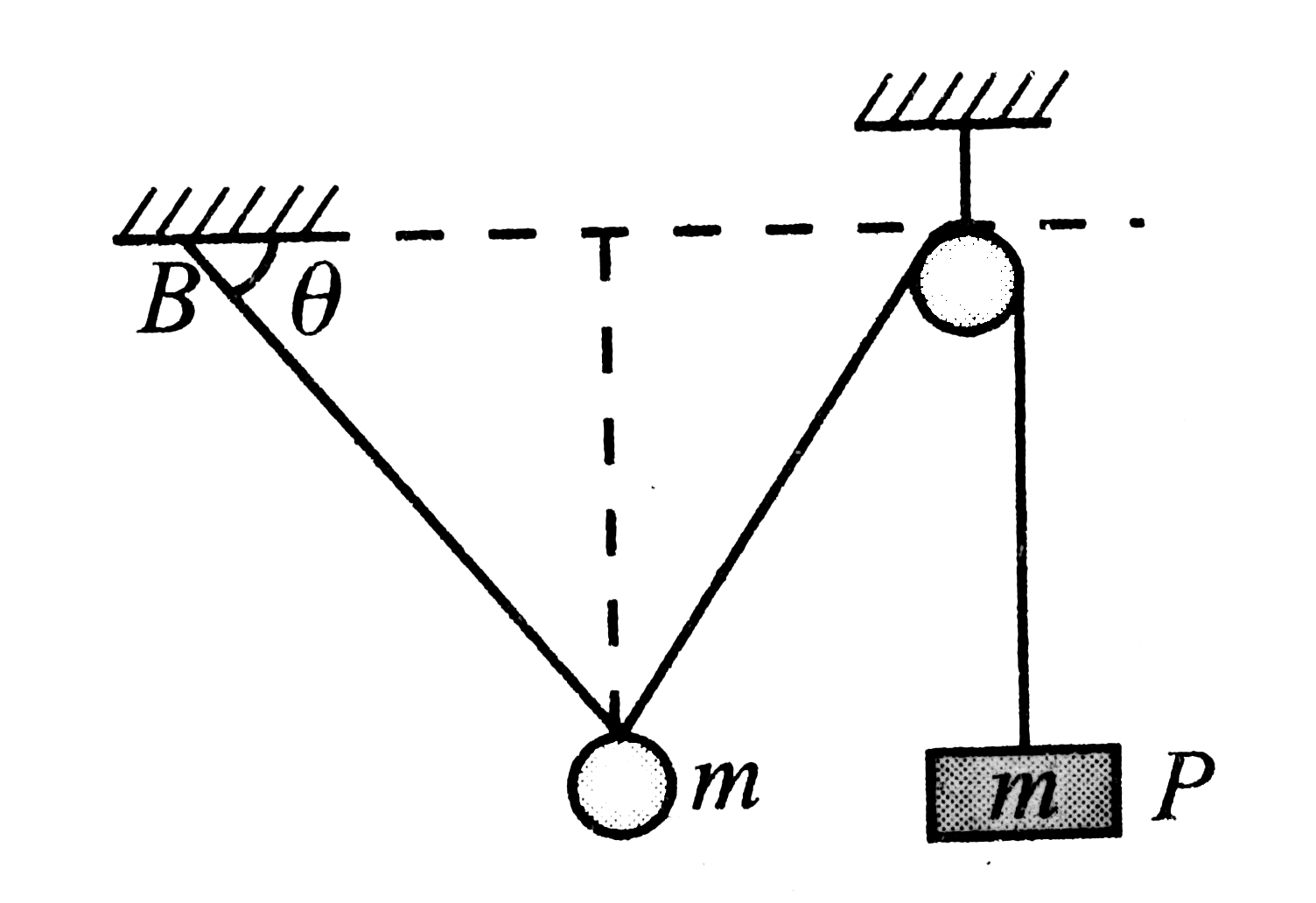If block 'C' mentioned above was released from some height and collided with 'P' with some velocity u, then find the velocity of the ring just after the collision. The collision is perfectly inelastic. View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
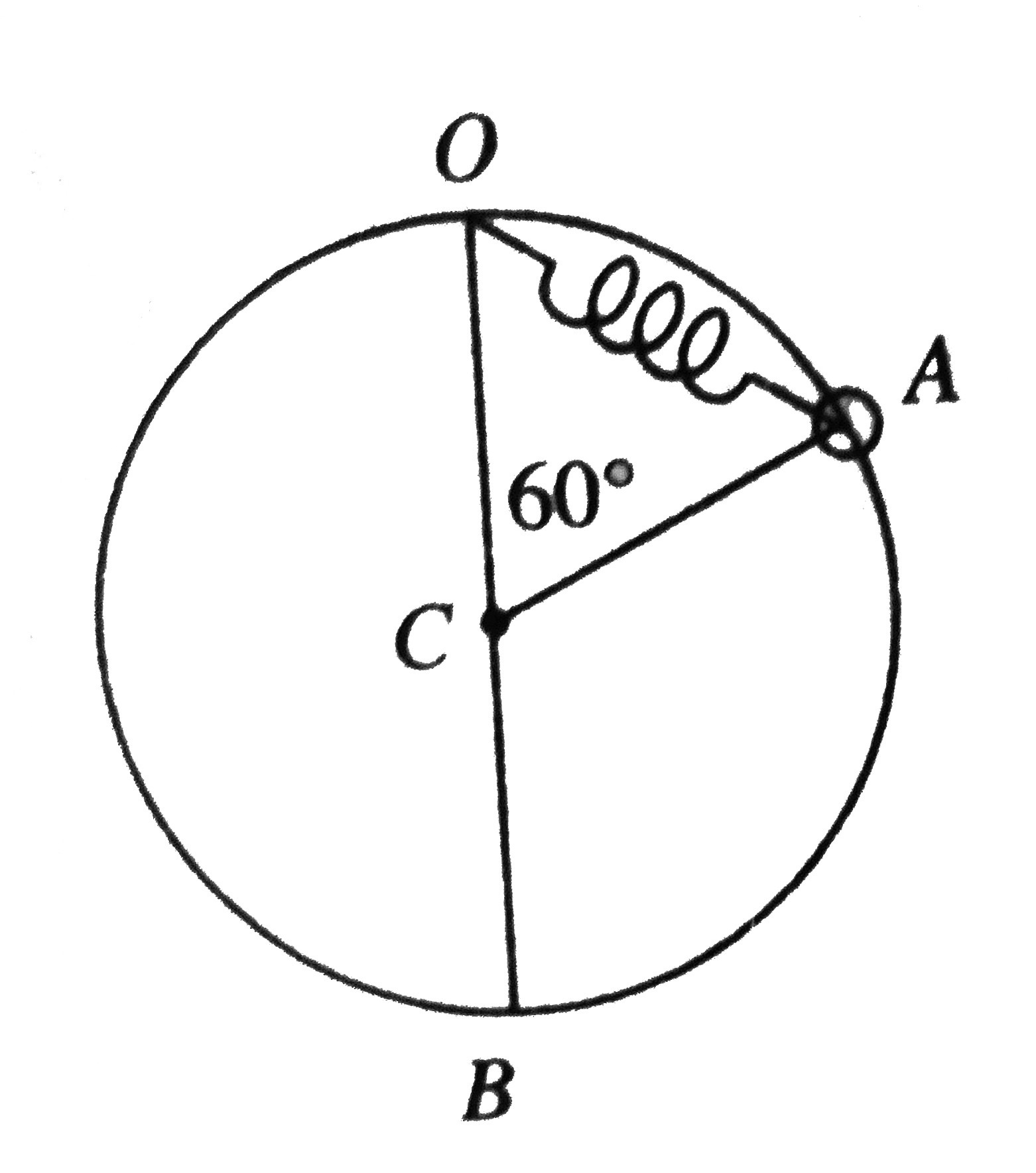
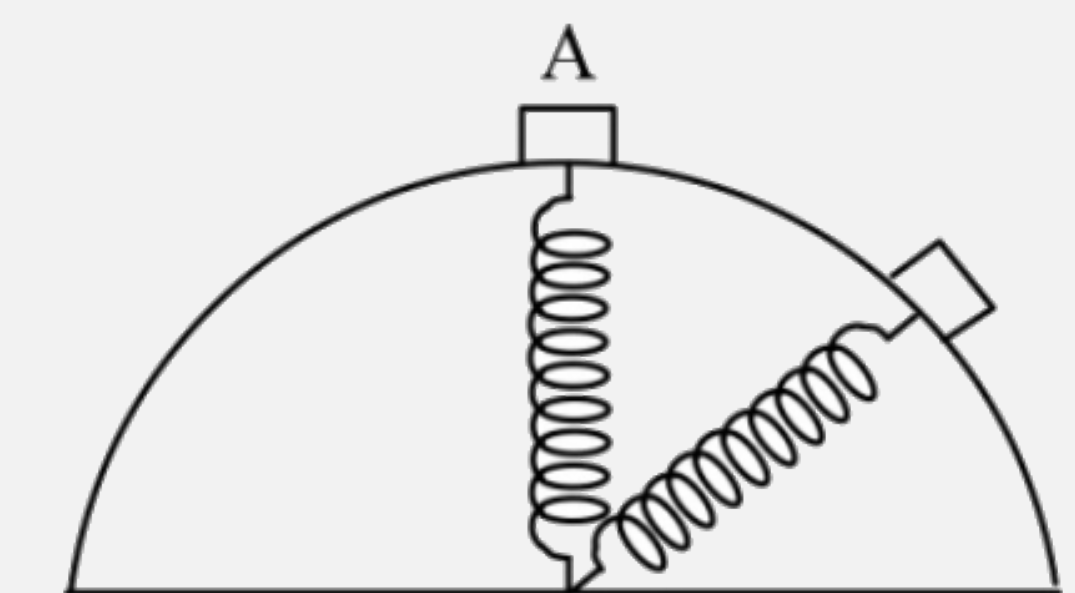
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View SolutionA conducting ring of mass m and radius r has a weightless conducting rod PQ of length 2r and resistance 2R attached to it along its diametre. It is pivoted at its centre C with its plane vertical, and two blocks of mass m and 2m are suspended by means of a light inextensible string passing over it as shown in Fig. The ring is free to rotate about C and the system is placed in magnetic field B (into the plane of the ring). A circuit is now complete by connecting the ring at A and C to a battery of emf V. It is found that for certain value of V , the system remains static.
In static condition, find the current through rod PC.View SolutionA thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as Bz=B0(1−αz) and Br=B0βr, where B0,α and β are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius r0 and self inductance L. Assume the acceleration due to gravity as g.
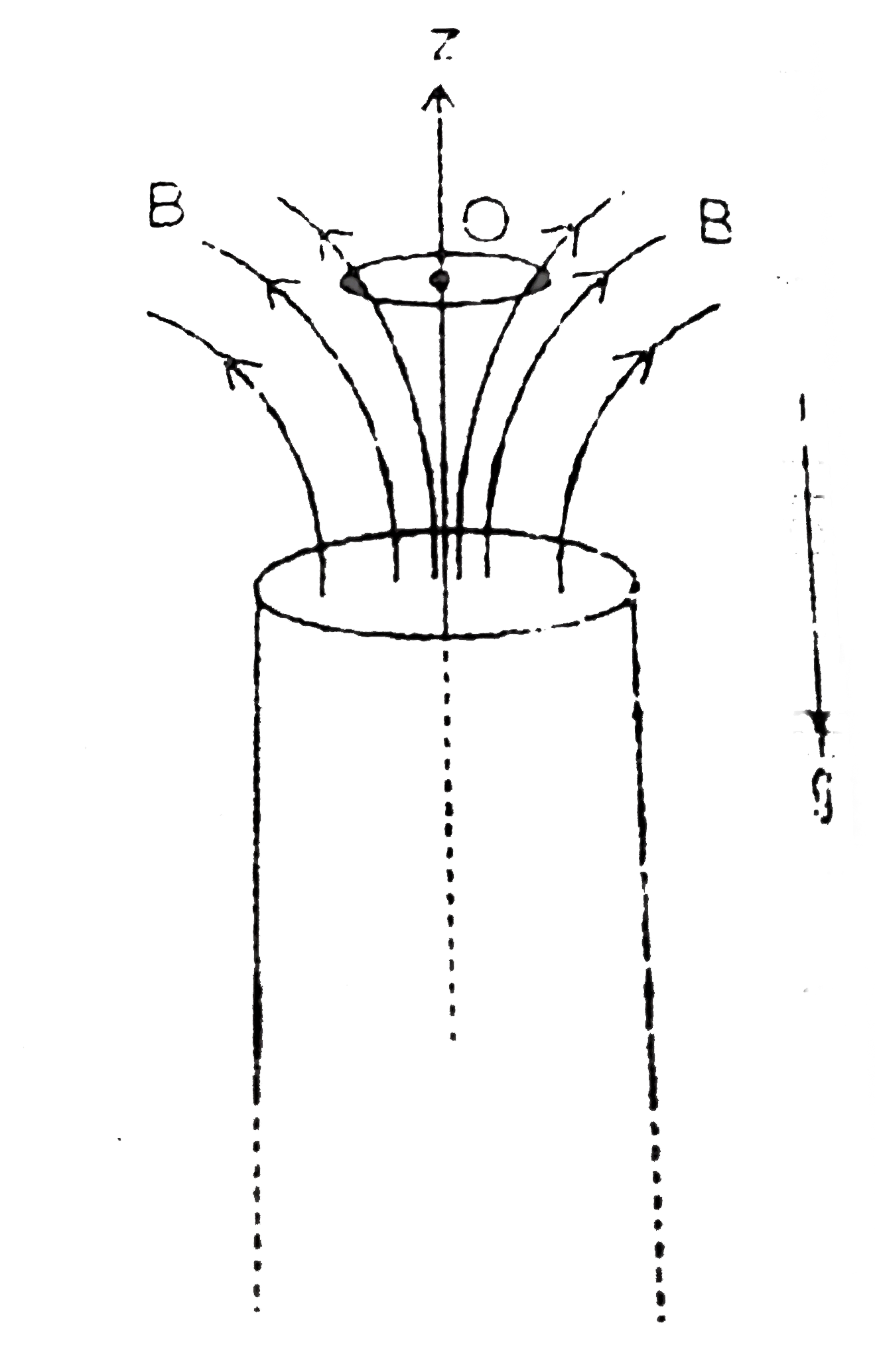
Find the vertical coordinates z for equilibrium position of the ring.View Solution