A wooden box is placed on a table. The normal force on the box from the table is N1. Now another identical box is kept on first box and the normal force on lower block due to upper block is N2 and normal force on lower block by the table is N3. For this situtation, mark out the correct statement (s).
N1=N2=N3
N1<N2=N3
N1=N2<N3
N1=N2>N3
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the wooden boxes placed on the table. Let's break it down step by step.
Step 1: Analyze the forces on the first box (lower box)
When only one box is placed on the table, the forces acting on it are:
- The gravitational force acting downwards, which is equal to its weight mg.
- The normal force N1 acting upwards from the table.
Since the box is in equilibrium (not moving), the normal force must balance the weight of the box. Therefore, we can write the equation:
N1=mg
Step 2: Analyze the forces on the second box (upper box)
Now, when a second identical box is placed on top of the first box, we need to consider the forces acting on the upper box:
- The gravitational force acting downwards on the upper box, which is also mg.
- The normal force N2 acting upwards from the lower box.
For the upper box to be in equilibrium, the normal force N2 must balance the weight of the upper box:
N2=mg
Step 3: Analyze the forces on the lower box (combined system)
Now, we consider the forces acting on the lower box due to both boxes:
- The total weight acting downwards is the weight of both boxes, which is 2mg.
- The normal force N3 acting upwards from the table.
For the lower box to be in equilibrium, the normal force N3 must balance the total weight of both boxes:
N3=2mg
Step 4: Summarize the relationships between the normal forces
From the above analysis, we have:
1. N1=mg
2. N2=mg
3. N3=2mg
Conclusion
From the relationships derived:
- N1 (normal force from the table on the lower box) is equal to mg.
- N2 (normal force from the upper box on the lower box) is also equal to mg.
- N3 (normal force from the table on the lower box) is equal to 2mg.
Thus, we can conclude:
N1=N2<N3
Correct Statement
The correct statements regarding the normal forces are:
- N1=N2
- N1<N3
When only one box is placed on the table, the forces acting on it are:
- The gravitational force acting downwards, which is equal to its weight mg.
- The normal force N1 acting upwards from the table.
N1=mg
Now, when a second identical box is placed on top of the first box, we need to consider the forces acting on the upper box:
- The gravitational force acting downwards on the upper box, which is also mg.
- The normal force N2 acting upwards from the lower box.
N2=mg
Now, we consider the forces acting on the lower box due to both boxes:
- The total weight acting downwards is the weight of both boxes, which is 2mg.
- The normal force N3 acting upwards from the table.
N3=2mg
From the above analysis, we have:
1. N1=mg
2. N2=mg
3. N3=2mg
From the relationships derived:
- N1 (normal force from the table on the lower box) is equal to mg.
- N2 (normal force from the upper box on the lower box) is also equal to mg.
- N3 (normal force from the table on the lower box) is equal to 2mg.
N1=N2<N3
The correct statements regarding the normal forces are:
- N1=N2
- N1<N3
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A book of mass 5 kg is placed on a table and it is pressed by 10 N force then normal force exerted by the table on the book is
View SolutionFor the two blocks shown in the adjacent figure, an external force of 18N is applied on the lower block. Find the acceleratiion of the upper block.
View SolutionA block of weight 9.8N is placed on a table. The table surface exerts an upward force of 10N on the block. Assume g=9.8m/s2.
View SolutionA small block of mass 20kg rests on a bigger block of mass 30kg, which lies on a smooth horizontal plane. Initially the whole system is at rest. The coefficient of friction between the blocks is 0.5. The horizontal force F=50N is applied on the lower block.
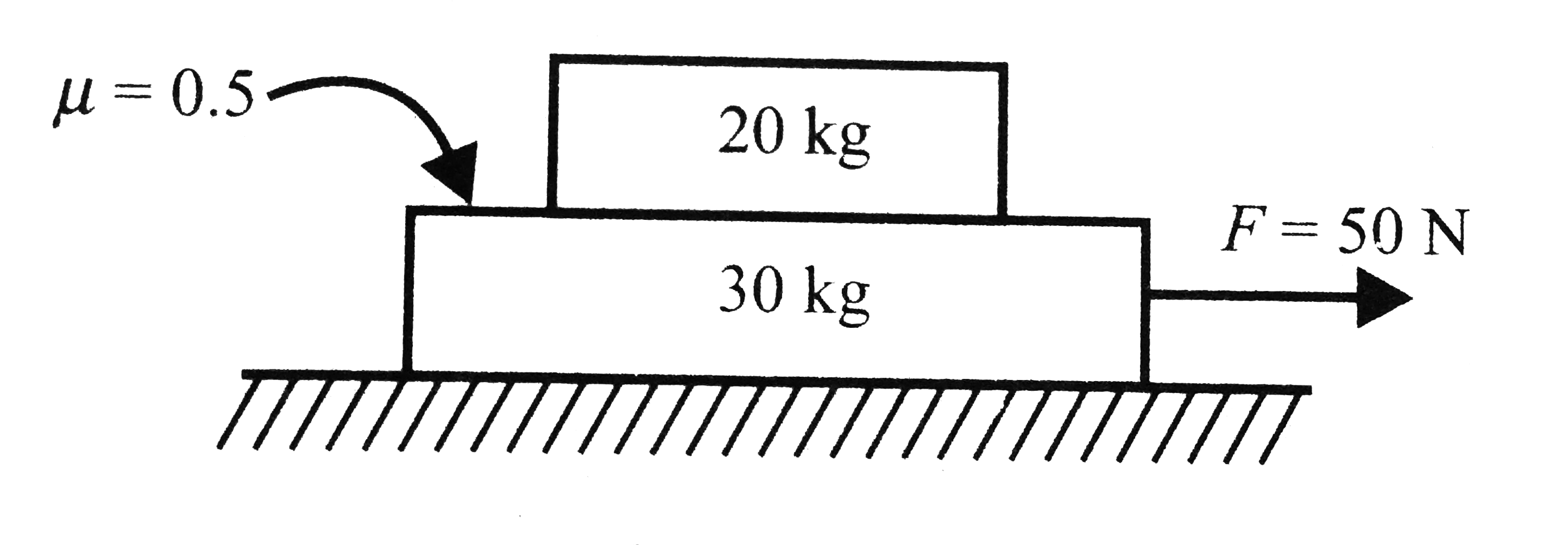
a. Find the work done by fricitonal force on upper block and on the lower block in t=2s.
b. Is the magnitude of work done by the frictional force on upper and lower blocks same?
c. Is the work done by the frictional force on the upper block converted to heat or mechanical energy or both?
View SolutionThese questions consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following four responses
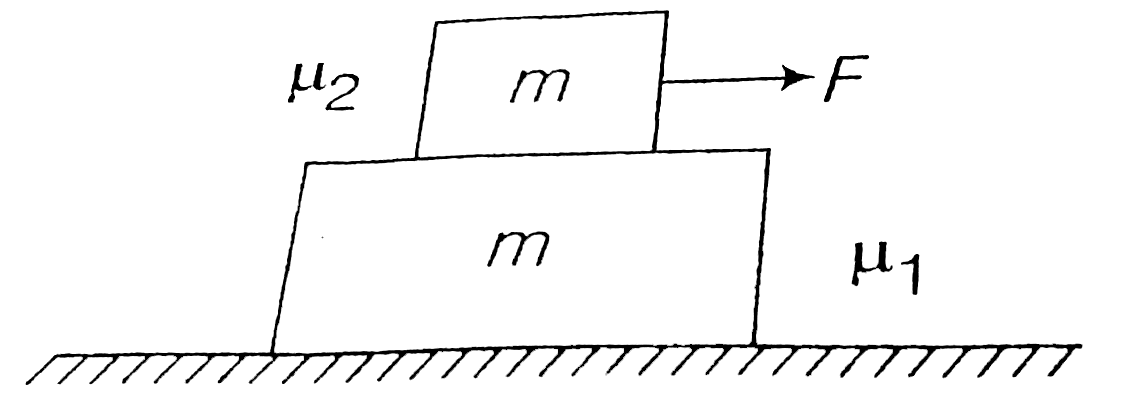
Assertion In the system of two blocks of equla masses as shown, the coefficient of friction between the blocks (μ2) is less than coefficient of friction (μ1) between lower block and ground. For all values of force F applied on upper block, lower block remains at rest.
Reason Frictional force on lower block due to upper block is not sufficient to overcome the frictional force on lower block due to ground.
View SolutionA block is kept at the corner of two walls and force 3N is applied on block. If μ=0.1, between block and walls then frictional force acting on block equal to :−
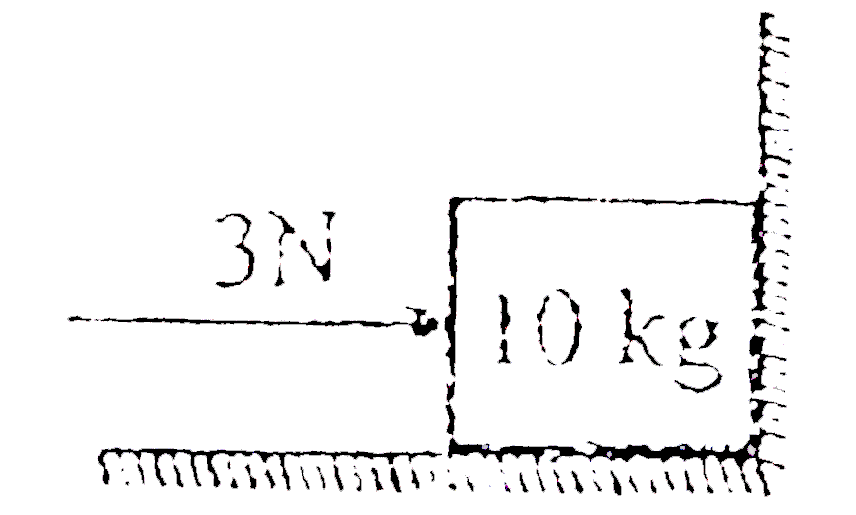
View SolutionThree block of masses 1kg, 4kg and 2kg are placed on a smooth horizontal plane as shown in figure. Find
(a) the acceleration of the system,
(b) the normal force between 1kg block and 4kg block,
( c) the net force on 2kg block

View SolutionFind the acceleration of the block and magnitude and direction of frictional force between block A and table, if block A is pulled towards Left with a force of 50 N.

View SolutionBlocks are in contact on a frictionless table. A horizontal force F=3N is applied to one block as shown. The force exerted by the smaller block m2 on block m1 is :
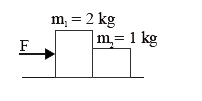
View SolutionThe figure shows a horizontal force →F acting on a block of mass M on an inclined plane (angle θ). What is the normal reaction N on the block?

View Solution