In an experiment on the determination of young's Modulus of a wire by Searle's method , following data is available:
Normal length of the wire (L)=110cm
Diameter of the wire (d)=0.01cm
Elongation in the wire (l)=0.125cm
This elongation is for a tension of 50N. The least counts for corresponding quantities are 0.01cm,0.00005cm,and0.001cm , respectively. Calculate the maximum error in calculating the value of Young's modulus (Y).
The correct Answer is:1.809%
To calculate the maximum error in determining Young's modulus (Y) using the given data, we can follow these steps:
Step 1: Understand the formula for Young's Modulus
Young's modulus (Y) is defined as:
Y=F⋅LA⋅l
where:
- F = Force applied (in Newtons)
- L = Original length of the wire (in cm)
- A = Cross-sectional area of the wire (in cm²)
- l = Elongation of the wire (in cm)
Step 2: Calculate the Cross-sectional Area (A)
The cross-sectional area A of the wire can be calculated using the diameter d:
A=πd24
Given d=0.01cm:
A=π(0.01)24=π×0.00014≈7.85×10−5cm2
Step 3: Identify the least counts and calculate relative errors
The least counts for the measurements are:
- Length L: ΔL=0.01cm
- Elongation l: Δl=0.001cm
- Diameter d: Δd=0.00005cm
Relative error in each quantity:
1. Relative error in Length L:
Relative error in L=ΔLL=0.01110≈9.09×10−5
2. Relative error in Elongation l:
Relative error in l=Δll=0.0010.125=0.008
3. Relative error in Diameter d:
Relative error in d=Δdd=0.000050.01=0.005
Step 4: Calculate the maximum error in Young's Modulus
The formula for the maximum error in Y is given by:
ΔYY=ΔLL+Δll+2⋅Δdd
Substituting the values:
ΔYY=9.09×10−5+0.008+2⋅0.005
=9.09×10−5+0.008+0.01
=0.0180909
Step 5: Convert to percentage error
To convert the relative error to percentage:
Percentage error=ΔYY×100≈1.80909%
Final Answer
The maximum error in calculating the value of Young's modulus Y is approximately 1.81%.
---
Young's modulus (Y) is defined as:
Y=F⋅LA⋅l
where:
- F = Force applied (in Newtons)
- L = Original length of the wire (in cm)
- A = Cross-sectional area of the wire (in cm²)
- l = Elongation of the wire (in cm)
The cross-sectional area A of the wire can be calculated using the diameter d:
A=πd24
Given d=0.01cm:
A=π(0.01)24=π×0.00014≈7.85×10−5cm2
The least counts for the measurements are:
- Length L: ΔL=0.01cm
- Elongation l: Δl=0.001cm
- Diameter d: Δd=0.00005cm
1. Relative error in Length L:
Relative error in L=ΔLL=0.01110≈9.09×10−5
Relative error in l=Δll=0.0010.125=0.008
Relative error in d=Δdd=0.000050.01=0.005
The formula for the maximum error in Y is given by:
ΔYY=ΔLL+Δll+2⋅Δdd
Substituting the values:
ΔYY=9.09×10−5+0.008+2⋅0.005
=9.09×10−5+0.008+0.01
=0.0180909
To convert the relative error to percentage:
Percentage error=ΔYY×100≈1.80909%
The maximum error in calculating the value of Young's modulus Y is approximately 1.81%.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Single Correct
Explore 93 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Multiple Correct
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Exercise 1.3
Explore 17 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
The original length of wire is (153.7±0.6)cm. It is streched to (155.3±0.2) cm. Calculate the elongation in the wire with error limits.
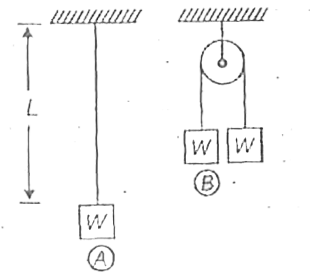
View SolutionIf in case A, elongation in wire of length L is l then for same wire elongation in case B will be
View SolutionThe length of a rectangular plate is measured by a meter scale and is found to be 10.0cm. Its width is measured by vernier calipers as 1.00cm. The least count of the meter scale and vernier calipers are 0.1cmand0.01cm respectively. Maximum permissibe error in area measurement is.
View SolutionThe length of a rectangular plate is measured by a meter scale and is found to be 10.0cm. Its width is measured by vernier callipers as 1.00cm. The least count of the meter scale and vernier calipers are 0.1cmand0.01cm respectively. Maximum permissibe error in area measurement is.
View SolutionA cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
View SolutionThe diameter of a sphere is 6cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
View SolutionThe diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0-2 cm. Find the length of the wire.
View SolutionA metal wire of length L, area of cross-section A and young's modulus Y is stretched by a variable force F such that F is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is l
View SolutionThe diameter of a sphere is measured as 1.71 cm using an instrument with a least count 0.01 cm What is the percentage error in its surface area?
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View Solution