In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.17 sec. The frequency of the wave is
1.47 Hz
0.36 Hz
0.73 Hz
2.94 Hz
The correct Answer is:A
To find the frequency of the sinusoidal wave given that the time required for a particular point to move from maximum displacement to zero displacement is 0.17 seconds, we can follow these steps:
1. Understanding the Motion: In a sinusoidal wave, the motion of a particle can be described in terms of its displacement over time. The maximum displacement (amplitude) occurs at the peak of the wave, and the zero displacement occurs at the equilibrium position.
2. Identifying the Time Interval: The time taken for a particle to move from maximum displacement (amplitude) to zero displacement is given as 0.17 seconds. This movement corresponds to one-quarter of the wave's period (T), as the particle moves from the peak to the equilibrium position.
3. Relating Time to Period: Since the time taken to move from maximum displacement to zero is T/4, we can set up the equation:
T4=0.17 seconds
4. Calculating the Period (T): To find the total period (T), we multiply both sides of the equation by 4:
T=0.17×4=0.68 seconds
5. Finding the Frequency (f): The frequency (f) of a wave is the reciprocal of the period (T). Thus, we can calculate the frequency as follows:
f=1T=10.68
6. Calculating the Frequency: Performing the calculation gives:
f≈1.47 Hz
Final Answer:
The frequency of the wave is approximately 1.47 Hz.
---
T4=0.17 seconds
T=0.17×4=0.68 seconds
f=1T=10.68
f≈1.47 Hz
The frequency of the wave is approximately 1.47 Hz.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:NDA EXAM QUESTIONS
Explore 55 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OSCILLATIONS
Explore 23 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
In a sinusoidal wave the time required for a particular point to move from equilibrium position to maximum displacement is 0.17s, then the frequency of wave is:
View SolutionWhen a sound wave of frequency 300 Hz passes through a medium the maximum displacement of a particle of the medium is 0.1 cm . The maximum velocity of the particle is equal to
View SolutionIf the number of waves from a source is passing a point is 30 in a second, what is the frequency of the wave?
View SolutionA string fixed at both ends is vibrating such that a point at quarter of its length from one end is a point of maximum displacement. The frequency of vibration in this mode is 100Hz. If the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum displacement is 100k then find the value of k.
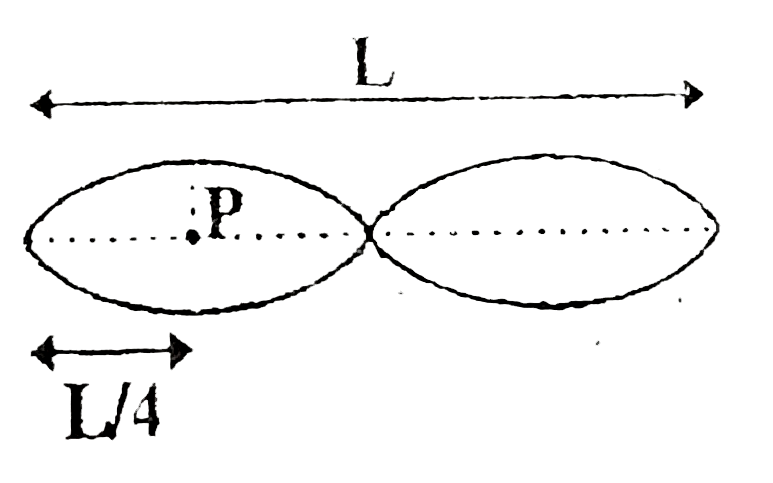
View SolutionA string fixed at both is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum displacement . The frequency of vibration emitted when it vibrates in the next mode such that this point is again a point of maximum displacement ?
View SolutionA sine wave is travelling in a medium. A particular partile has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
View SolutionA travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidal. The amplitude of vibration is 1.0cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10kgm−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0 the end x= 0 is at its positive extreme position. Write the wave equation. (c ) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10ms.
View SolutionShows the shape of a progressive wave at time t=0. after a time t=(1)/(80), the particle at the origin has its maximum negative displacement.if the wave speed is 80 units maximum negative displacement. If the wave speed is 80 units, then find the equation of the progressive wave.
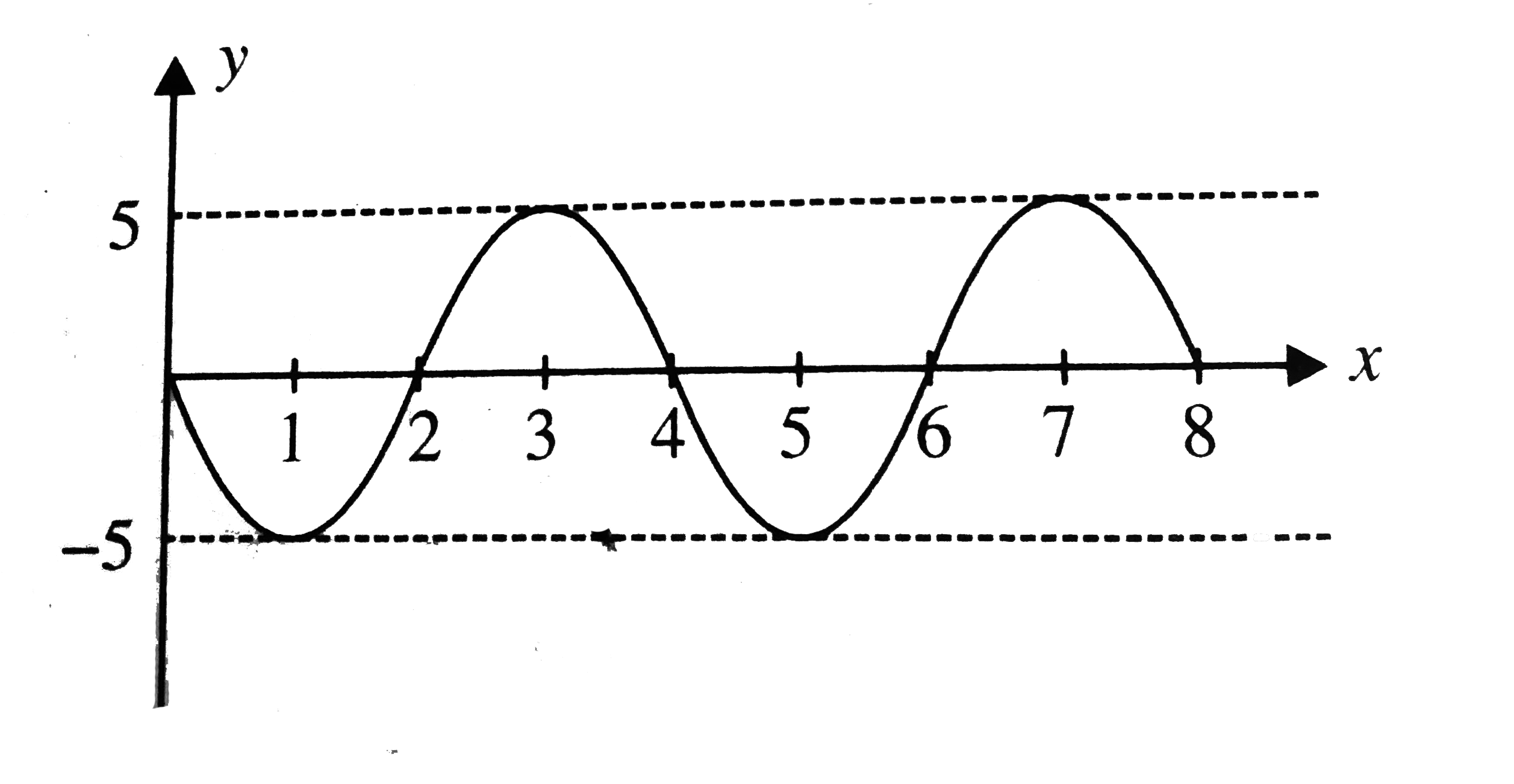 .
.
View SolutionAssertion : In longitudinal wave pressure is maximum at a point where displacement is zero .
Reason : There is a phase difference of π2 between y(x,t) and ΔP(x,t) equation in case of longitudinal wave.
View SolutionThe equation of a wave travelling on a string is y=(0.10mm)sin[3.14m−1)x+(314s−1)t]. (a) In which direction does the wave travel ? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string ?
View Solution

