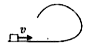
A small block is shot into each of the four track as shown in Fig 15.7.1. Each of the track rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in



The correct Answer is:a
To solve the problem of determining which track has the maximum normal reaction at the highest point, we can follow these steps:
1. Understanding the Forces at the Highest Point:
At the highest point of the track, the forces acting on the block are:
- The gravitational force (weight) acting downward, mg.
- The normal reaction force N acting downward.
2. Centripetal Force Requirement:
For the block to move in a circular path, there must be a net inward (centripetal) force. This force is provided by the normal force and the weight of the block. The centripetal force required is given by:
Fc=mv2r
where m is the mass of the block, v is the speed of the block, and r is the radius of curvature of the track at that point.
3. Setting Up the Equation:
At the highest point, the centripetal force is provided by the normal force and the weight of the block:
mv2r=N+mg
Rearranging gives us the expression for the normal force:
N=mv2r−mg
4. Maximizing the Normal Force:
To maximize the normal force N, we need to minimize the radius r of the track. The smaller the radius, the larger the value of mv2r will be, thus increasing N.
5. Comparing Different Tracks:
Since all tracks rise to the same height and the speed of the block entering each track is the same, we need to analyze the radius of curvature for each track. The track with the smallest radius of curvature will yield the maximum normal reaction.
6. Conclusion:
Based on the analysis, the track with the smallest radius of curvature will have the maximum normal reaction at the highest point.
Final Answer:
The maximum normal reaction occurs in the track with the smallest radius of curvature.
At the highest point of the track, the forces acting on the block are:
- The gravitational force (weight) acting downward, mg.
- The normal reaction force N acting downward.
For the block to move in a circular path, there must be a net inward (centripetal) force. This force is provided by the normal force and the weight of the block. The centripetal force required is given by:
Fc=mv2r
where m is the mass of the block, v is the speed of the block, and r is the radius of curvature of the track at that point.
At the highest point, the centripetal force is provided by the normal force and the weight of the block:
mv2r=N+mg
Rearranging gives us the expression for the normal force:
N=mv2r−mg
To maximize the normal force N, we need to minimize the radius r of the track. The smaller the radius, the larger the value of mv2r will be, thus increasing N.
Since all tracks rise to the same height and the speed of the block entering each track is the same, we need to analyze the radius of curvature for each track. The track with the smallest radius of curvature will yield the maximum normal reaction.
Based on the analysis, the track with the smallest radius of curvature will have the maximum normal reaction at the highest point.
The maximum normal reaction occurs in the track with the smallest radius of curvature.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:UNIFORM CIRCULAR MOTION (ROTATIONAL MOTION AND MOMENT OF INERTIA )
Explore 25 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:GRAVITATION
Explore 25 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:MOTION IN FLUIDS
Explore 25 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
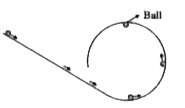
A ball of mass 100 g is made to loop-the-loop in a vertical circle as shown in Fig. 7.1.29. The radius of the circle is 0.5 m (i)-What is the critical velocity at the highest point of the track ? (ii) If the velocity of the ball at the highest point of the track is twice the critical velocity what is the force exerted by the ball against track?
View SolutionA block is released from A on a frictionless track as shown in Fig. 7.2.6. What is the magnitude of radial acceleration and the total acceleration of the block at B ?
View SolutionA small ball is rolled with speed u from piont A along a smooth circular track as shown in figure. If x=3R, then

Determine the required speed u so that the ball returns to A, the point of projection after passing through C, the highest point.
View SolutionA flexible track is fixed in two alternative arrangements, as shown in the figure. A toy car is released at rest and slides down the track air resistance can be ignored. The length of the track used is the same in each case and the height through which it falls from the bench to the floor is the same.


codes:
View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
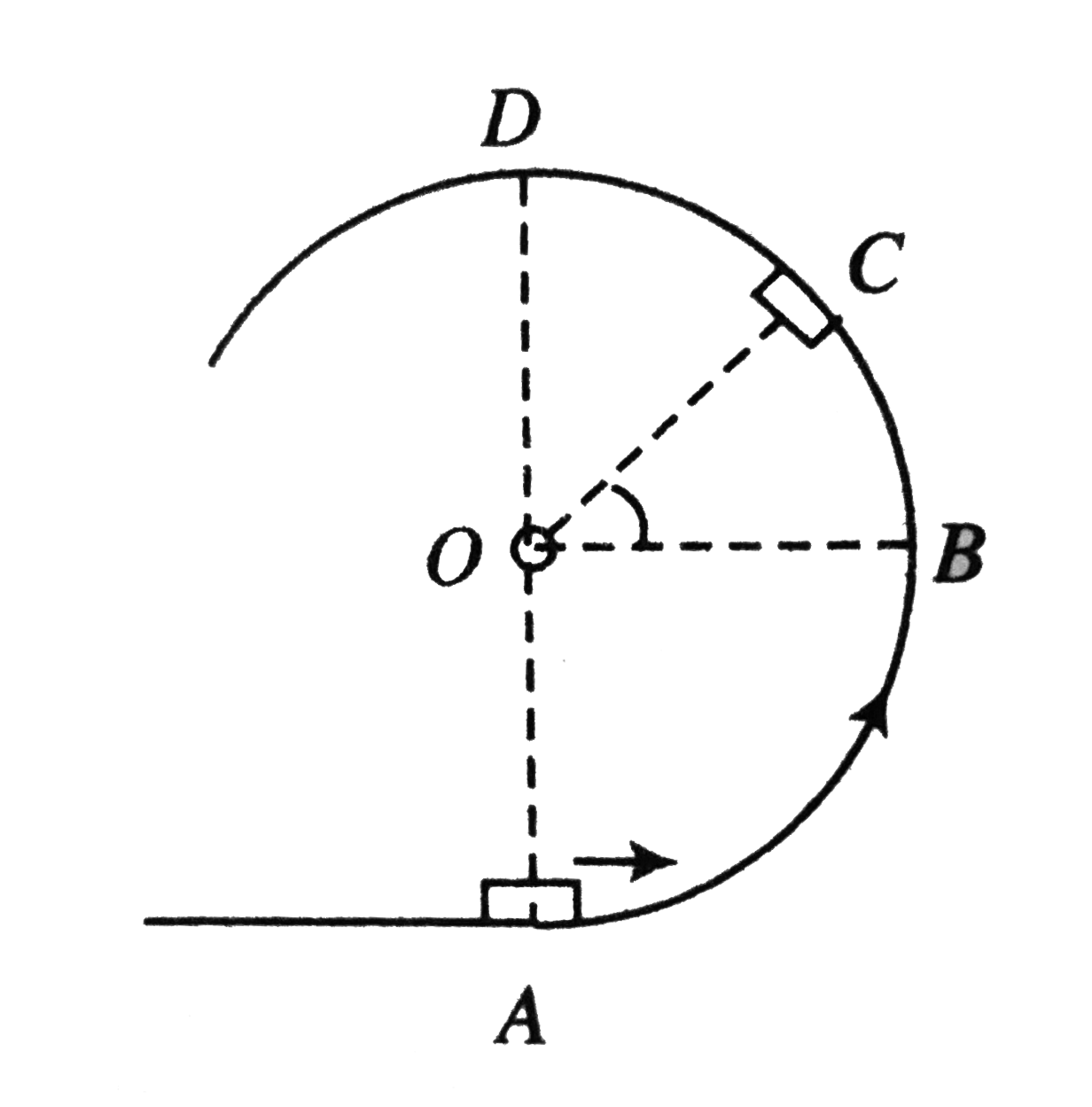
Find where the maximum contact force occurs between the block and the track.
View SolutionBlock of mass m are released from rest and they slide down the inclined surface as shown in figure. Show that the work done by the frictional forces on the blocks are same in all the cases. Also calculate the speeds with which the blocks reach point B. The coefficient of friction for all the surface is μk.

View SolutionA small ball is rolled with speed u from piont A along a smooth circular track as shown in figure. If x=3R, then

What is the minimum value of x for which the ball can reach the point of projection after reaching C?
View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
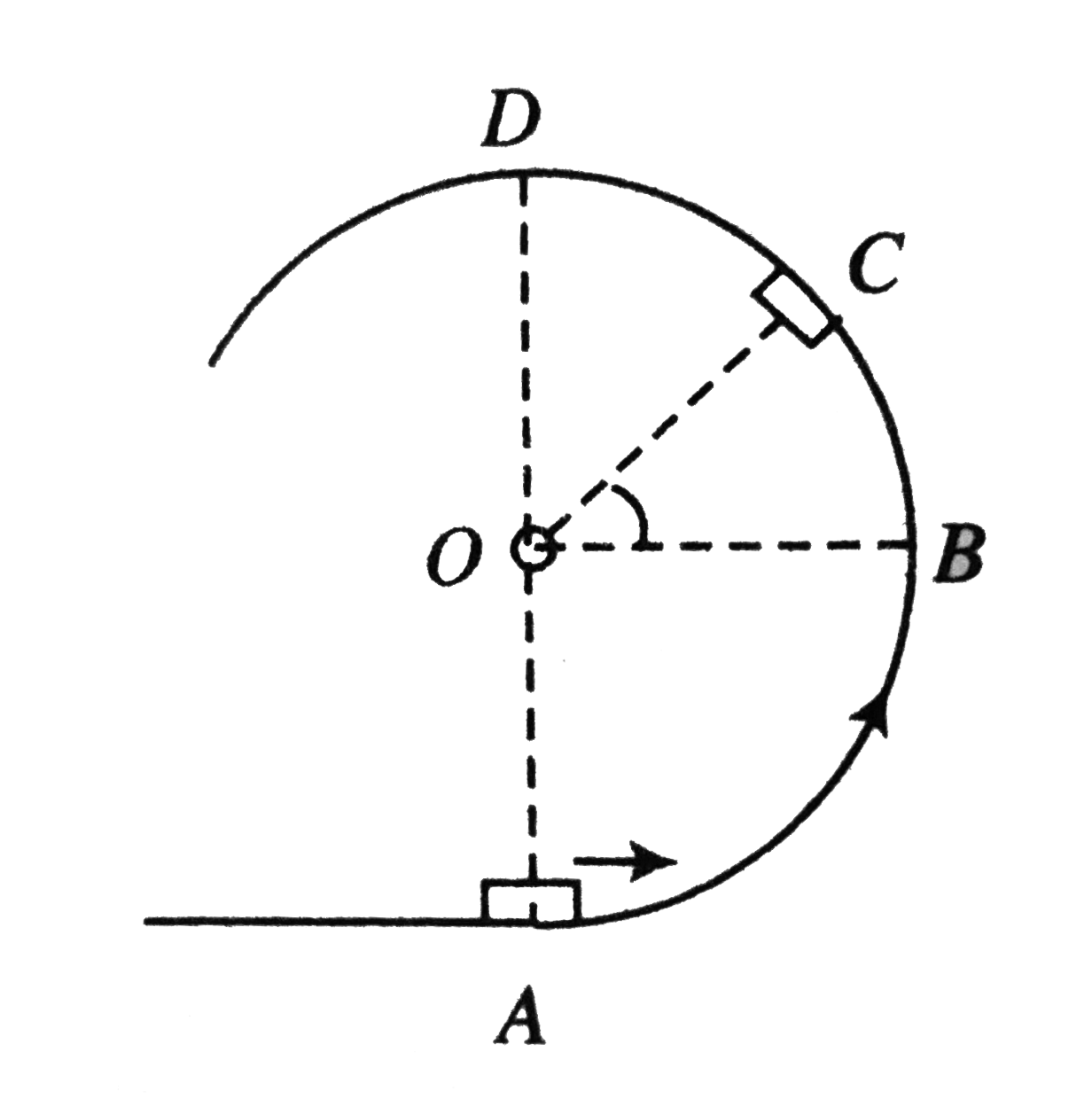
At what angle θ with horizontal does the block gets separated from the track?
View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.

At what angle θ with horizontal does the block gets separated from the track?
View SolutionA block of mass m slides along a frictionless surfce as shown in the figure. If it is releases from rest from A what is its speed at B?

View Solution

