Question

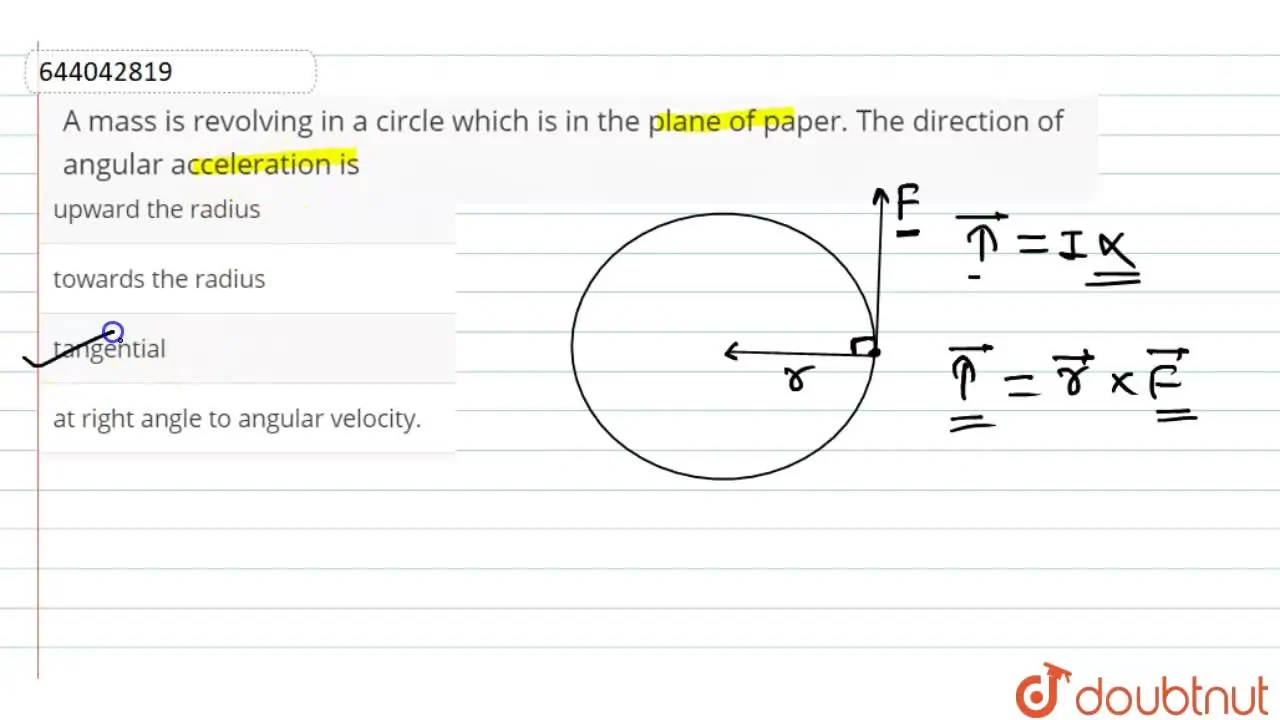
A mass is revolving in a circle which is in the plane of paper. The direction of angular acceleration is

Options

A. upward the radius
B. towards the radius
C. tangential
D. at right angle to angular velocity.

Answer

C

Explanation

To solve the question regarding the direction of angular acceleration for a mass revolving in a circle in the plane of paper, we can follow these steps:

Step 1: Understand the Motion
A mass revolving in a circle experiences circular motion. In circular motion, there are two types of acceleration: centripetal acceleration (which is directed towards the center of the circle) and tangential acceleration (which is directed along the tangent to the circle).

Hint: Remember that circular motion can involve both centripetal and tangential components of acceleration.

Step 2: Identify the Forces
In circular motion, the forces acting on the mass can include a centripetal force (which keeps the mass moving in a circle) and a tangential force (which can change the speed of the mass). The tangential force is responsible for angular acceleration.

Hint: Think about how forces affect the speed of an object in circular motion.

Step 3: Relate Torque and Angular Acceleration
Torque (\( \tau \)) is related to angular acceleration (\( \alpha \)) through the equation:
\( \tau = I \alpha \)
where \( I \) is the moment of inertia. The direction of torque is the same as the direction of angular acceleration when the force is applied tangentially.

Hint: Recall that torque is the rotational equivalent of linear force.

Step 4: Determine the Direction of Angular Acceleration
If the force applied to the mass is tangential to the circle, then the torque will also be tangential. Since the direction of torque is the same as the direction of angular acceleration, we conclude that the angular acceleration is also directed tangentially to the circle.

Hint: Visualize the circular motion and where the tangential force would act.

Step 5: Conclusion
Thus, the direction of angular acceleration for a mass revolving in a circle in the plane of paper is tangential to the circle.

Final Answer: The direction of angular acceleration is tangential.