The ratio rotational and translational kinetic energies of a sphere is
2/9
2/7
2/5
7/2
The correct Answer is:B
To find the ratio of rotational and translational kinetic energies of a sphere, we can follow these steps:
Step 1: Write the formulas for kinetic energies
- The rotational kinetic energy K1 is given by the formula:
K1=12Iω2
where I is the moment of inertia and ω is the angular velocity.
- The translational kinetic energy K2 is given by the formula:
K2=12mv2
where m is the mass and v is the linear velocity.
Step 2: Find the moment of inertia for a sphere
- The moment of inertia I for a solid sphere is:
I=25mr2
where r is the radius of the sphere.
Step 3: Substitute the moment of inertia into the rotational kinetic energy formula
- By substituting the expression for I into the equation for K1:
K1=12(25mr2)ω2=15mr2ω2
Step 4: Relate angular velocity to linear velocity
- We know that the angular velocity ω is related to the linear velocity v by:
ω=vr
Therefore, substituting ω in terms of v into the equation for K1:
K1=15mr2(vr)2=15mr2v2r2=15mv2
Step 5: Substitute into the translational kinetic energy formula
- Now, we can express K2 in terms of v:
K2=12mv2
Step 6: Find the ratio of rotational to translational kinetic energy
- Now we can find the ratio K1K2:
K1K2=15mv212mv2
- The mv2 terms cancel out:
K1K2=1/51/2=25
Final Result
The ratio of rotational to translational kinetic energy of a sphere is:
K1K2=25
- The rotational kinetic energy K1 is given by the formula:
K1=12Iω2
where I is the moment of inertia and ω is the angular velocity.
K2=12mv2
where m is the mass and v is the linear velocity.
- The moment of inertia I for a solid sphere is:
I=25mr2
where r is the radius of the sphere.
- By substituting the expression for I into the equation for K1:
K1=12(25mr2)ω2=15mr2ω2
- We know that the angular velocity ω is related to the linear velocity v by:
ω=vr
Therefore, substituting ω in terms of v into the equation for K1:
K1=15mr2(vr)2=15mr2v2r2=15mv2
- Now, we can express K2 in terms of v:
K2=12mv2
- Now we can find the ratio K1K2:
K1K2=15mv212mv2
- The mv2 terms cancel out:
K1K2=1/51/2=25
The ratio of rotational to translational kinetic energy of a sphere is:
K1K2=25
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:GRAVITATION
Explore 25 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:PROPERTIES OF MATTER (ELASTICITY )
Explore 22 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:UNIFORM CIRCULAR MOTION
Explore 25 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
A small sphere of mass 1 kg is rolling without slipping with linear speed
v=√2007m/s

It leaves the inclined plane at point C.
Find ratio of rotational and translational kinetic energy of the sphere when it strikes the ground after leaving from point C.
View SolutionThe ratio of translational and rotational kinetic energies at 100K temperature is 3:2. Then the internal energy of one mole gas at that temperature is (R=8.3j/mol−K]
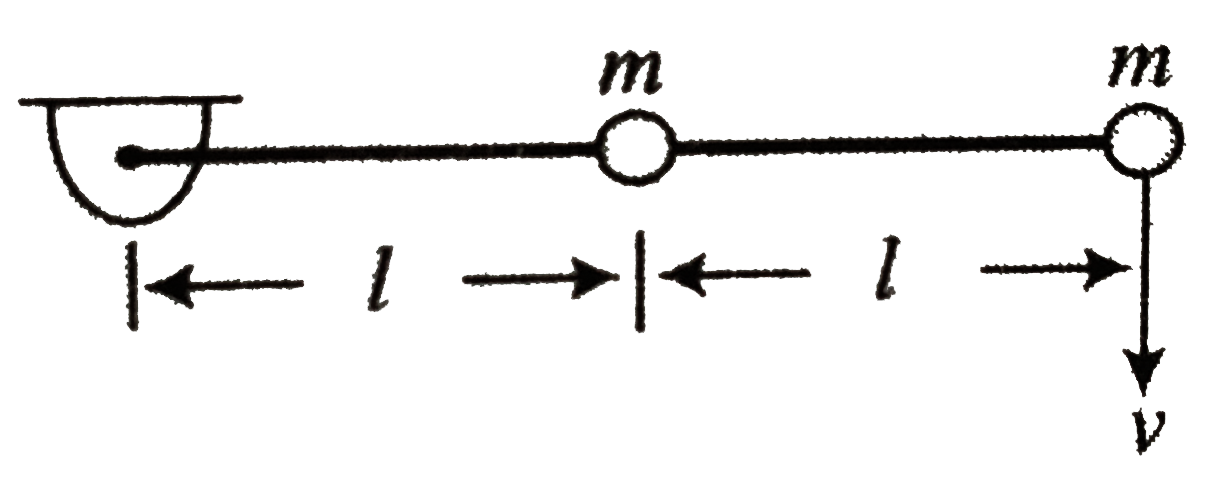
View SolutionTwo beads each of mass m are welded at the ends of two light rigid rods each of length l. if the pivots are smooth, find the ratio of translational and rotational kinetic energy of system.
View SolutionA ring is rolling on an inclined plane. The ratio of the linear and rotational kinetic energies will be
View Solution(a) What is the average translational kinetic energy of a molecule of an ideal gas at temperature of 276∘C ?
(a) What is the total random translational kinetic energy of the molecules in one mole of this gas ?
( c) What is the rms speed of oxygen molecules at this temperature ?
View SolutionAn ideal gas is in a container of volume V0 at pressure P0 If the same amount of gas is in container of volume 3V0 at pressure P0. then the ratio of final average translational kinetic energy to the initial average translational kinetic energy of the gaseous molecule is
View SolutionA ring is rolling on an inclined plane. The ratio of the linear and rotational kinetic energies will be?
View SolutionThe translational kinetic energy of an ideal gas depends only its
View SolutionIf R is the radius of gyration of a body of mass M and radius r, then the ratio of its rotational to translational kinetic energy in the rolling condition is
View SolutionUnder forward slip condition, translational kinetic energy of a ring is greater than its rotational kinetic energy is this statement true of false?
View Solution

