A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
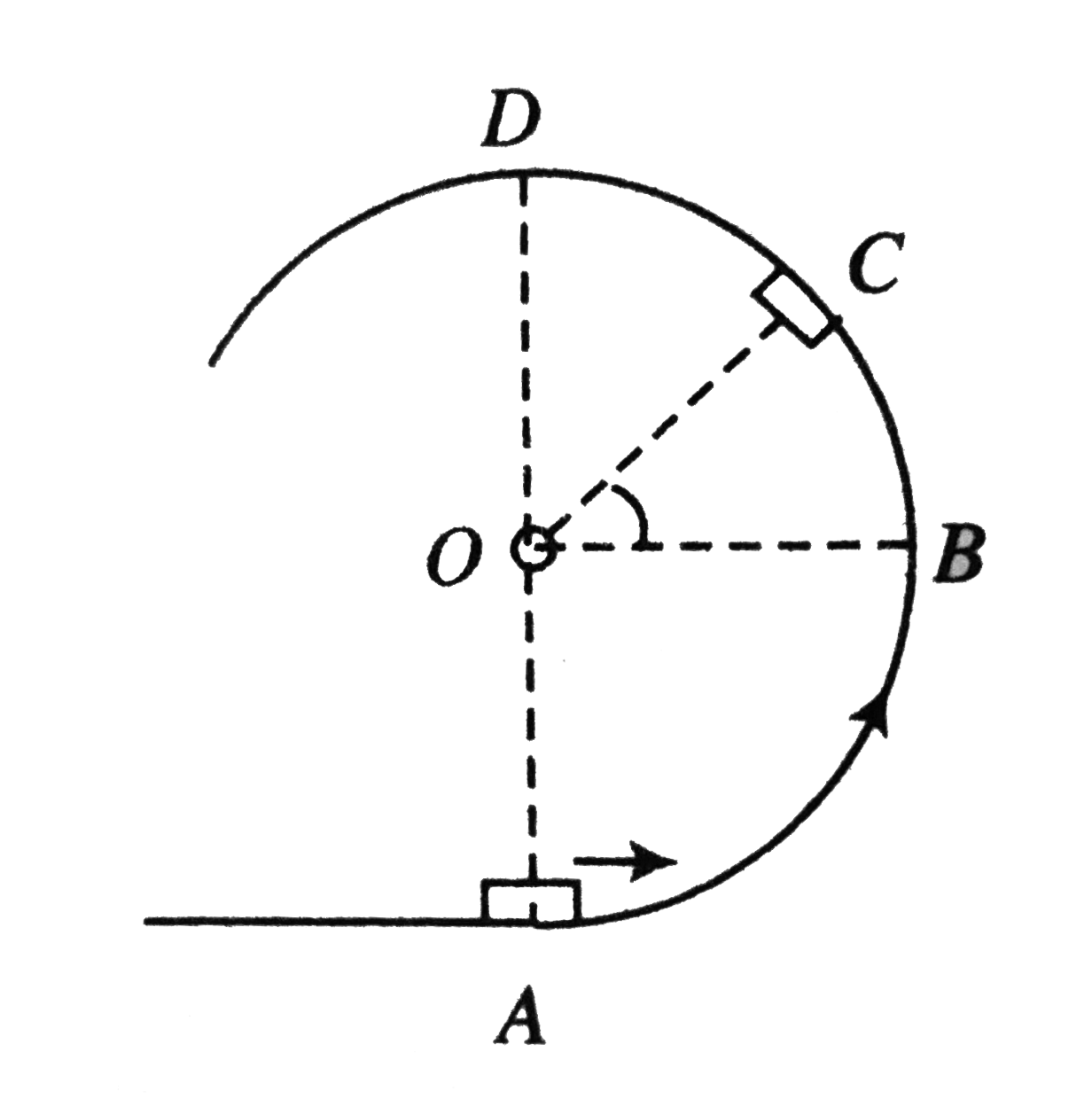
At what angle θ with horizontal does the block gets separated from the track?
(a) sin−1(13)
(b) sin−1(34)
(c) sin−1(23)
(d) never leaves contact with the track
The correct Answer is:C
v1=2√5√5gR=2√gR
Now, v22=v21−2g(R+Rsinθ)=2gR−2gRsinθ
N+mgsinθ=mv22R
Put N=0
⇒mgsinθ=m2g(1−sinθ)
⇒sinθ=23
⇒θ=sin−1(23)

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
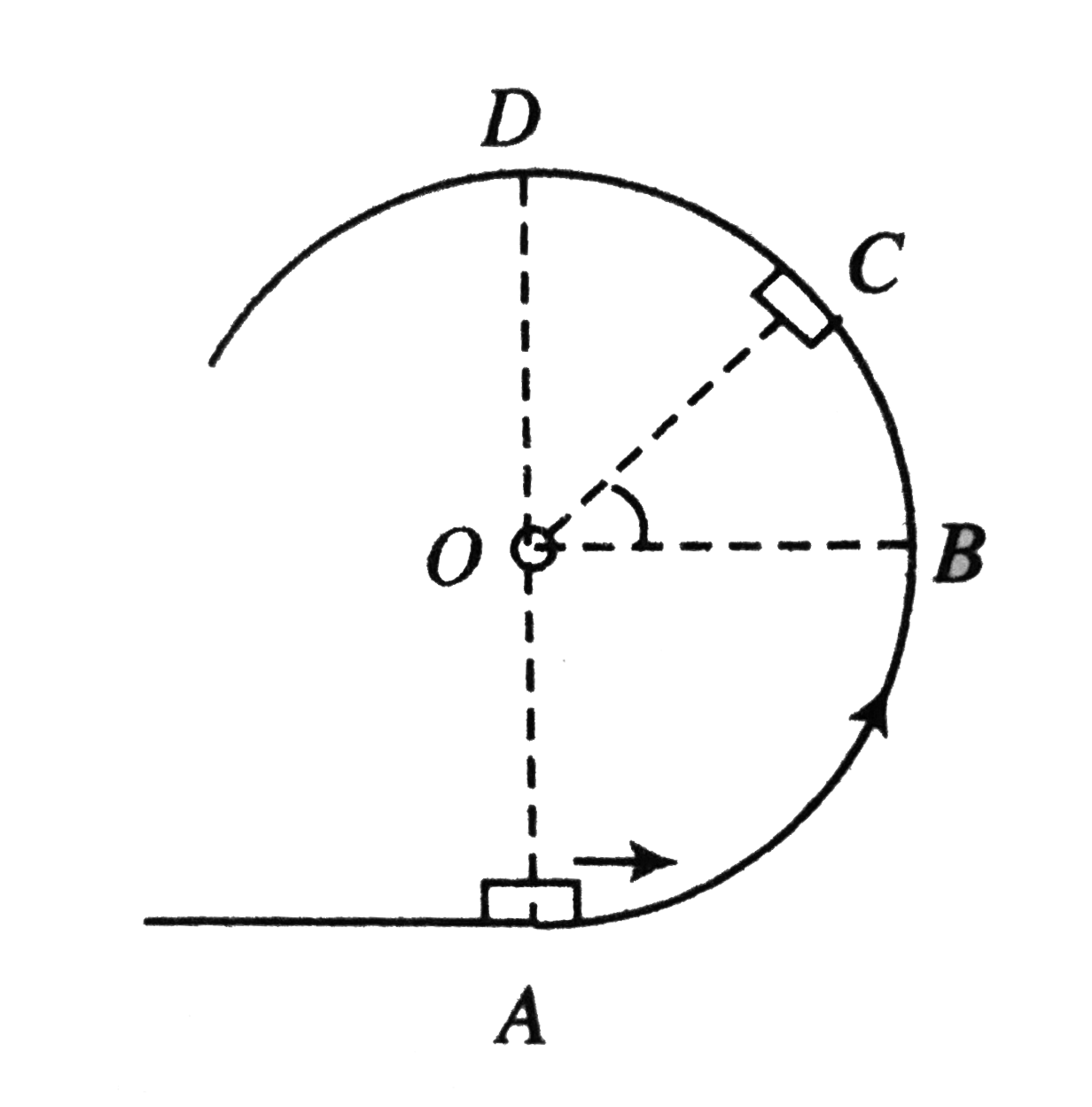
Find where the maximum contact force occurs between the block and the track.
View Solution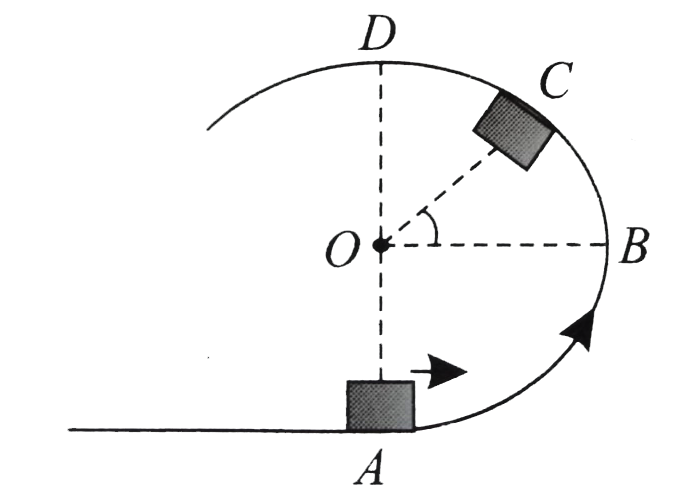
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
Q. When the block reaches the point B, what is the direction (in terms of angle with horizontal) of acceleration of the block?
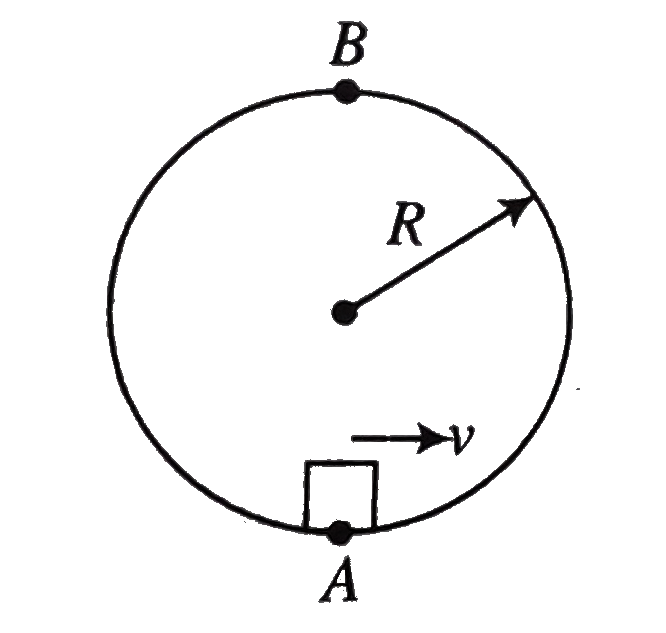
View SolutionA block of mass m is projected on a smooth horizontal circular track with velocity v what is the average normal force exered by the circular walls on the block during motion A to B?
View SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA block of mass m is released along a smooth track shown in figure from its top point. Find the word done by gravity during its downward motion to the bottom of track.
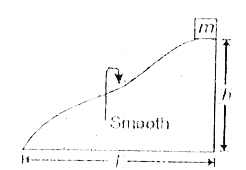
View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View SolutionA small block slides with velocity 0.5√gr on the horizontal frictionless surface as shown in the figure. The block leaves the surface at point C . Calculate angle θ in the figure.
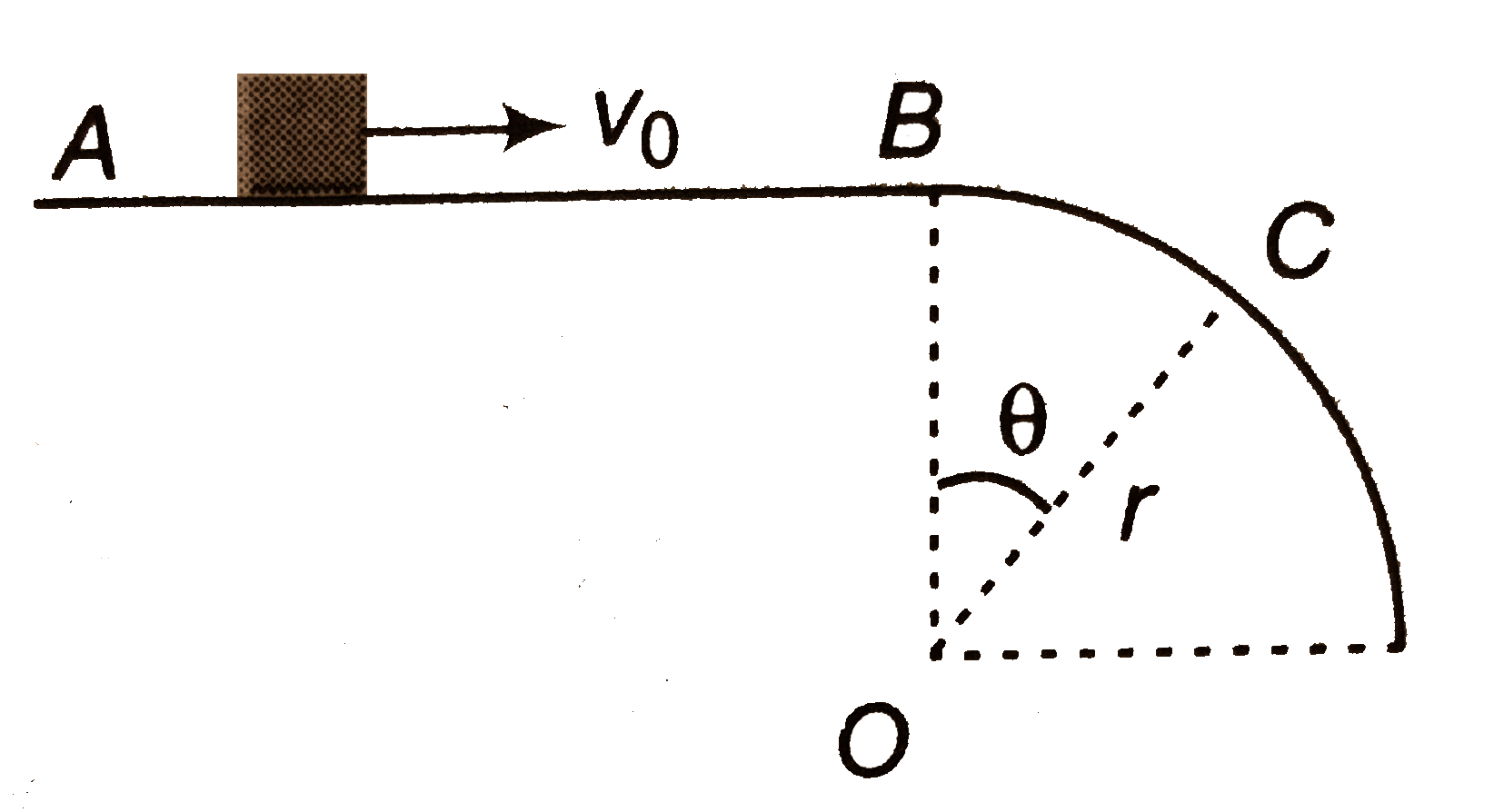
View Solution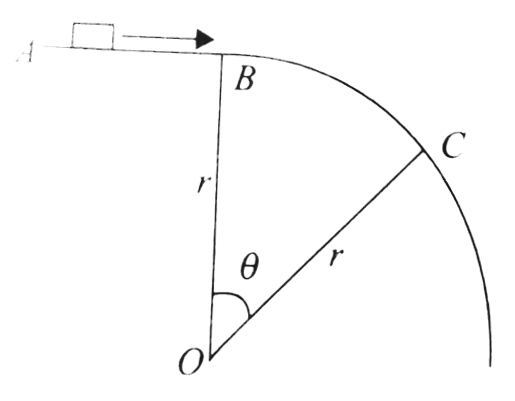
A small block slides with velocity v0=0.5√gr on the horizontal frictiohnless surface as shown in the fig. the block leaves the surface at point C. The angle θ in the figure is:
View SolutionFigure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
What minimum velocity should be imparted to a small block of same mass m so that it may each point B :
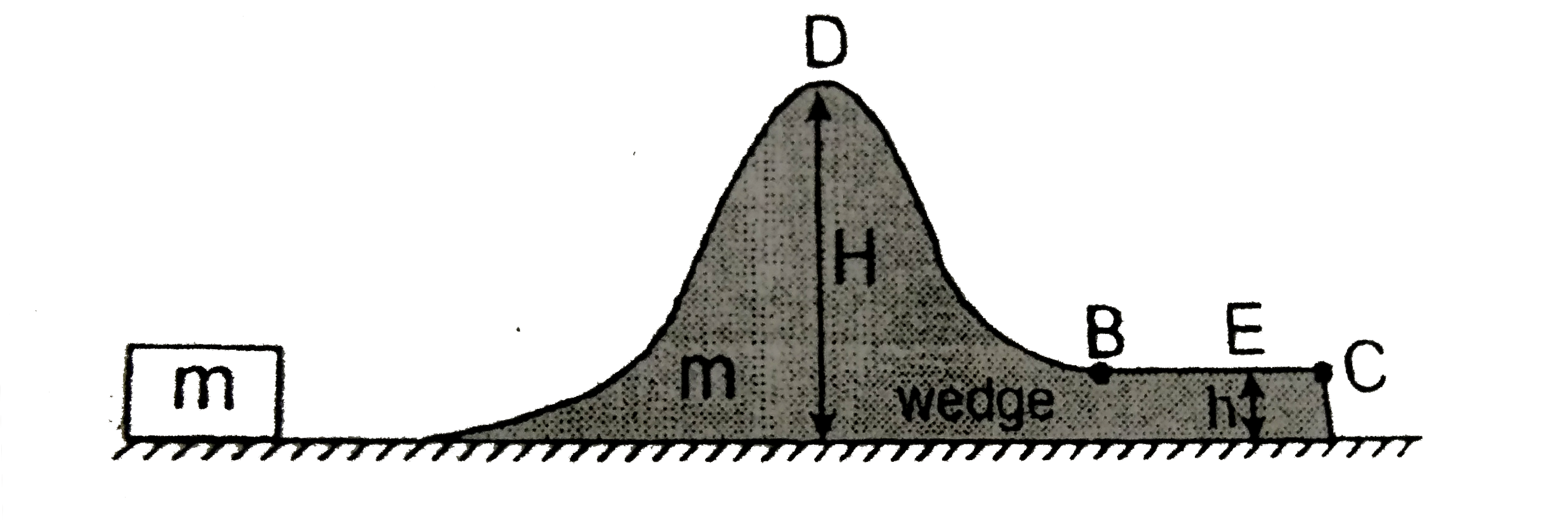
View Solution
