Two particles, 1 and 2, move with constant velocities v1 and v2. At the initial moment their radius vectors are equal to r1 and r2. How must these four vectors be interrelated for the particles to collide?
r1−r2|r1−r2|=v2−v1|v2−v1|
r2.v1=r2.r2
r1×v1=r2×v2
r1×v1=v1−v2
The correct Answer is:a
To determine how the vectors r1, r2, v1, and v2 must be interrelated for the two particles to collide, we can follow these steps:
Step 1: Define the position of the particles at the time of collision
Let the collision occur at point A with position vector RA. At time t, the position vectors of the two particles can be expressed as:
RA=r1+v1t
RA=r2+v2t
Step 2: Set the equations equal to each other
Since both expressions equal the position vector RA, we can set them equal:
r1+v1t=r2+v2t
Step 3: Rearrange the equation
Rearranging the equation gives us:
r1−r2=(v2−v1)t
Step 4: Solve for time t
From the rearranged equation, we can express t as:
t=r1−r2v2−v1
This equation implies that the time t must be a scalar quantity, which means the right-hand side must also be a scalar.
Step 5: Analyze the relationship of the vectors
For the two particles to collide, the vectors must satisfy the condition that the direction of r1−r2 is the same as the direction of v2−v1. This can be expressed as:
r1−r2|r1−r2|=v2−v1|v2−v1|
Conclusion
The final relationship that must hold for the particles to collide is:
r1−r2|r1−r2|=v2−v1|v2−v1|
Let the collision occur at point A with position vector RA. At time t, the position vectors of the two particles can be expressed as:
RA=r1+v1t
RA=r2+v2t
Since both expressions equal the position vector RA, we can set them equal:
r1+v1t=r2+v2t
Rearranging the equation gives us:
r1−r2=(v2−v1)t
From the rearranged equation, we can express t as:
t=r1−r2v2−v1
This equation implies that the time t must be a scalar quantity, which means the right-hand side must also be a scalar.
For the two particles to collide, the vectors must satisfy the condition that the direction of r1−r2 is the same as the direction of v2−v1. This can be expressed as:
r1−r2|r1−r2|=v2−v1|v2−v1|
The final relationship that must hold for the particles to collide is:
r1−r2|r1−r2|=v2−v1|v2−v1|
Similar Questions
Two particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionTwo particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
View SolutionTwo point masses 1 and 2 move with uniform velocities →v1 and →v2, respectively. Their initial position vectors are →r1 and →r2, respectively. Which of the following should be satisfied for the collision of the point masses?
View SolutionTwo particles AandB are moving with constant velocities v1andv2. At t=0, v1 makes an angle θ0 with the line joining AandBandv2 makes an angle θ2 with the line joining AandB.
(a) Find the condition for AandB to collide.
(b) Find the time after which AandB will collide if separation between them is d at t=0.
 .
.
View SolutionTwo particles A and B move with constant velocity →v1 and →v2 along two mutually perpendicular straight lines towards intersection point O as shown in figure, At moment t = 0 particles were located at distance l1 and l2 respectively from O. Then minimu distance between the particles and time taken are respectively
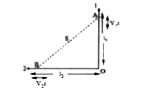
View SolutionTwo particles A and B are moving with constant velocities V1=ˆj and v2=2ˆi respectively in XY plane. At time t=0, the particle A is at co-ordinates (0,0) and B is at (-4,0). The angular velocities of B with respect to A at t=2s is (all physical quantities are in SI units)
View SolutionTwo particles of masses m1,m2 move with initial velocities u1 and u2. On collision, one of the particles get excited to higher level, after absording enegry. If final velocities of particles be v1 and v2 then we must have
View SolutionTwo particles of masses m1,m2 move with initial velocities u1andu2. On collision, one of the particles get excited to higher level, after absorbing energy ε. If final velocities of particles be v1 andv2, then we must have
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
View Solution

