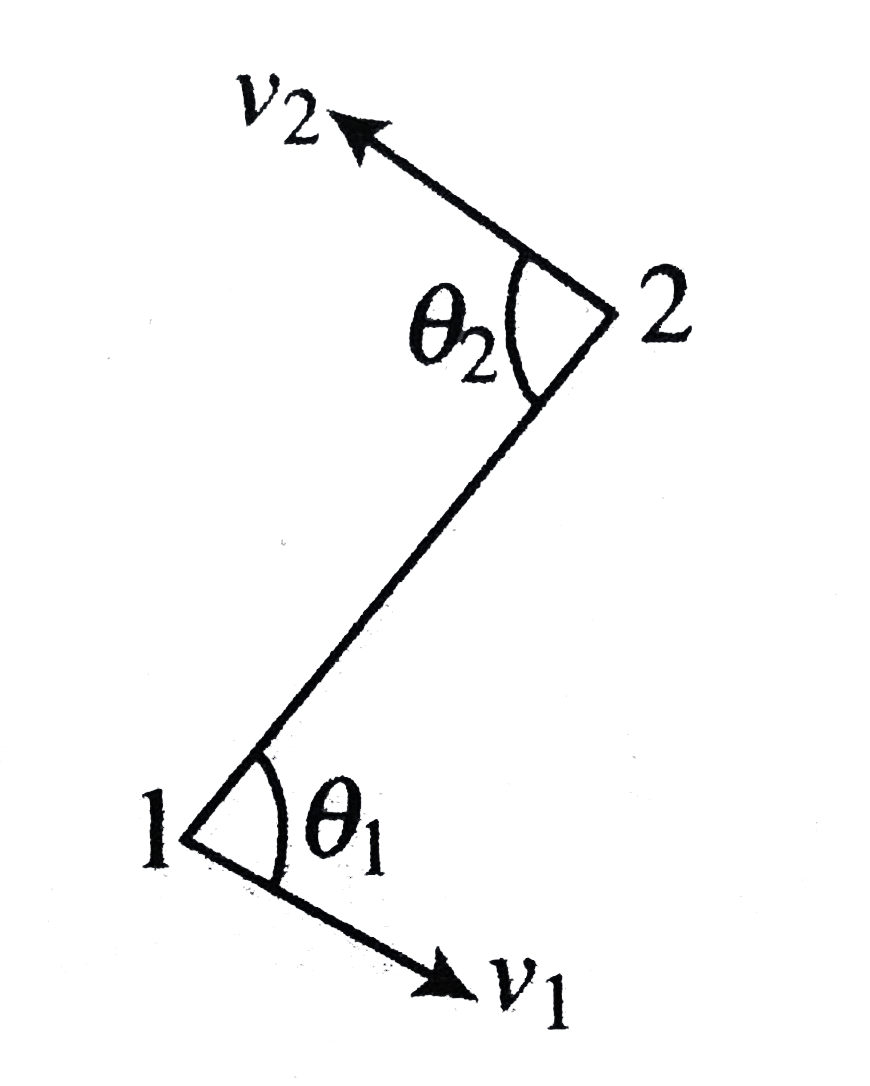
Two particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
Let us find the relative velocity between the particles perpendicular to the line joining them, the velocity of 1 relative to velocity of 2 is
→v12=→v1−→v2
Then, →v12y=→v1y−→v2y=−v1sinθ1ˆj−v2sinθ2ˆj
Hence, ω12=∣∣→v12y∣∣l
Substituting ∣∣→v12y∣∣, we have
ω12=v1sinθ1+v2sinθ2l.
 ,
, .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Subjective
Explore 40 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Single Correct
Explore 76 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.3
Explore 12 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
Two particles AandB are moving with constant velocities v1andv2. At t=0, v1 makes an angle θ0 with the line joining AandBandv2 makes an angle θ2 with the line joining AandB.
(a) Find the condition for AandB to collide.
(b) Find the time after which AandB will collide if separation between them is d at t=0.
 .
.
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionTwo particles are projected from the same point making angles angle θ1 and θ2 with the horizontal respectively in such a way that their horizontal velocities are equal. The ratio of maximum heights (H1H2) will be equal to
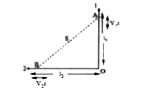
View SolutionTwo particles A and B move with constant velocity →v1 and →v2 along two mutually perpendicular straight lines towards intersection point O as shown in figure, At moment t = 0 particles were located at distance l1 and l2 respectively from O. Then minimu distance between the particles and time taken are respectively
View SolutionTwo particles, 1 and 2, move with constant velocities v1 and v2. At the initial moment their radius vectors are equal to r1 and r2. How must these four vectors be interrelated for the particles to collide?
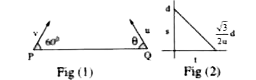
View SolutionA two particles P and Q are separated by distance d apart. P and Q move with velocity v and u making an angle 60∘ and θ with line PQ the graph between their relative separation (8) when time t is shown in figure (2). The velocity v in terms of u
View SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
The trajectory of particle 1 with respect to particle 2 wil be
View SolutionTwo particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.

View SolutionTwo masses, m1 and m2 , are moving with velocities v1 and v2. Find their total kinetic energy in the reference frame of centre of mass.
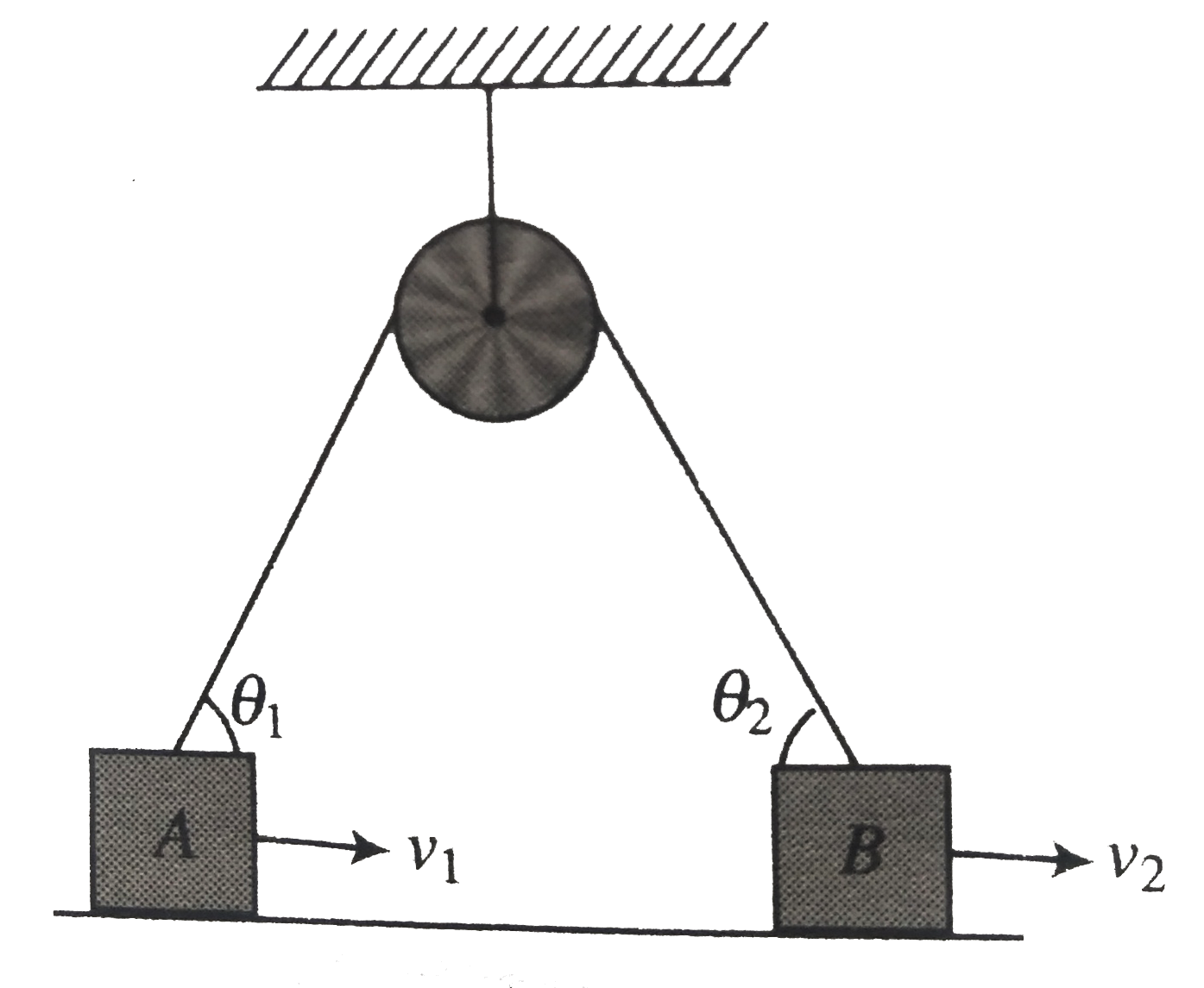
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
View Solution