Two particles 1 and 2 move with constant velocities ¯¯¯V1and¯¯¯V2. At the initial moment (t = 0 sec). Their position vectors are equal to ¯¯¯r1and¯¯¯r2. How must these four vectors be interrelated for the particles to collide.Solution in Telugu
¯r1−¯r2|¯r1−¯r2|=→V2−→V1∣∣→V2−→V1∣∣
Topper's Solved these Questions
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 9 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:NUMERICAL EXXERCISE (LEVEL -1)
Explore 12 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 4 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 6 Videos
Similar Questions
Find the components of vector ¯¯¯A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj
View SolutionA body of mass 5Kg moves under a force of 10ˆi+15ˆj−20ˆk . What is the acceleration produced?
View SolutionFour identical point charges are fixed at the four corners of a square of a side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large, distance along the line perpendicular to plane of square. The minimum value of initial velocity V0 in m/s required to cross the square is? (m=1gm.l=4√2m,Q=1μc,q=0.5μc)

View SolutionA fish is at a depth of 12 cm in water is viewed by an observer on the bank of a lake. To what height the image of the fish is raised in cm ?
View SolutionTwo particles, 1 and 2, move with constant velocities v_1 and v_2 . At the initial moment their radius vectors are equal to r_1 and r_2 . How must these four vectors be interrelated for the particles to collide?
View SolutionAt t=0, a particle at (1,0,0) moves towards point (4,4,12) with a constant velocity of magnitude 65m/s. The position of the particle is measured in metres and time in sec. Assuming constant velocity, the position of the particle at t=2sec is :
View SolutionA particle starts moving at t = 0 in a circle of radius R=2m with constant angular acceleration of a−3rad/sec2. Initial angular speed of the particle is 1 rad/sec. At time t0 the angle between the acceleration vector and the velocity vector of the particle is 37∘.
What is the value of t0 ?
View SolutionA particle starts moving at t = 0 in a circle of radius R = 2m with constant angular acceleration of a - 3 "rad/sec"^(2) . Initial angular speed of the particle is 1 rad/sec. At time t_(0) the angle between the acceleration vector and the velocity vector of the particle is 37^(@) . What is the magnitude of the acceleration of the particle at t_(0) ?
View Solutionयदि m द्रव्यमान वाले कण का स्थिति सदिश →r1 तथा 2m द्रव्यमान वाले कण का स्थिति सदिश →r2 हो, तो उस निकाय के द्रव्यमान- केन्द्र का स्थिति सदिश क्या होगा?
View SolutionTwo particles A and B, move with constant velocities →v1 and →v2. At the initial moment their position vectors are →r1 and →r2 respectively. The condition for particle A and B for their collision is
View SolutionThe magnitude of acceleration and velocity of a particle moving in a plane, whose position vector ¯r3t2ˆi+2tˆj+ˆk at t=2sec. are, respectively
View SolutionA particle starts from origin at time t=0 and moves in positive X - direction. Its velocity ¯v=10tˆi cm/ sec. The distance covered by the particle in 8 sec. will be
View Solutionकण की द्वि-विमीय गति में, कण बिन्दु A से स्थिति सदिश r1 तथा बिन्दु B से स्थिति सदिश r2 तक गति करता है। यदि इन सदिशों का परिमाण क्रमश: r1 = 3 तथा r2 = 4 तथा x अक्ष से बने कोण क्रमश: θ1=75∘ तथा 15∘ हैं। तब विस्थापित सदिश का परिमाण है
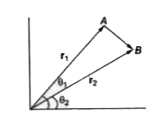
View SolutionTwo particle A and B, move with constant velocities vec(v_1) and vec(v_2) . At the initial moment their position vectors are vec(r_1) and vec(r_2) respectively . The condition for particles A and B for their collision is
View SolutionIf a moving particle have linear momentum →P and position vector →r then choose the correct relation between →→p and angular momentum →L of particle about the origin.
View Solution

