An electric bulb suspended from the roof of a train by a thread shifts through' an angle of 19.8° when the train goes round a curved path 100 m in radius. Find the speed of the train
The correct Answer is:18.78 m/s
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a bulb suspended from the roof of a train, which shifts at an angle of 19.8° when the train moves in a circular path of radius 100 m. We need to find the speed of the train.
Step 2: Draw the Free Body Diagram (FBD)
- Draw the bulb hanging from the roof of the train.
- The tension (T) in the thread acts at an angle of 19.8° with the vertical.
- The weight (mg) of the bulb acts downward.
Step 3: Resolve the Tension into Components
- The vertical component of tension: Tcos(19.8°)
- The horizontal component of tension (providing centripetal force): Tsin(19.8°)
Step 4: Set Up the Equations
1. The vertical forces balance:
Tcos(19.8°)=mg(Equation 1)
2. The horizontal forces provide the centripetal force:
Tsin(19.8°)=mv2r(Equation 2)
Step 5: Divide the Two Equations
To eliminate T, divide Equation 2 by Equation 1:
Tsin(19.8°)Tcos(19.8°)=mv2rmg
This simplifies to:
tan(19.8°)=v2rg
Step 6: Solve for the Speed (v)
Rearranging gives:
v2=rgtan(19.8°)
Taking the square root:
v=√rgtan(19.8°)
Step 7: Substitute the Values
Given:
- r=100m
- g=9.8m/s2
- θ=19.8°
Now substitute these values into the equation:
v=√100×9.8×tan(19.8°)
Step 8: Calculate the Value
First, calculate tan(19.8°):
tan(19.8°)≈0.361
Now substitute:
v=√100×9.8×0.361
Calculating this gives:
v=√353.378≈18.7m/s
Final Answer
The speed of the train is approximately 18.7m/s.
---
We have a bulb suspended from the roof of a train, which shifts at an angle of 19.8° when the train moves in a circular path of radius 100 m. We need to find the speed of the train.
- Draw the bulb hanging from the roof of the train.
- The tension (T) in the thread acts at an angle of 19.8° with the vertical.
- The weight (mg) of the bulb acts downward.
- The vertical component of tension: Tcos(19.8°)
- The horizontal component of tension (providing centripetal force): Tsin(19.8°)
1. The vertical forces balance:
Tcos(19.8°)=mg(Equation 1)
2. The horizontal forces provide the centripetal force:
Tsin(19.8°)=mv2r(Equation 2)
To eliminate T, divide Equation 2 by Equation 1:
Tsin(19.8°)Tcos(19.8°)=mv2rmg
This simplifies to:
tan(19.8°)=v2rg
Rearranging gives:
v2=rgtan(19.8°)
Taking the square root:
v=√rgtan(19.8°)
Given:
- r=100m
- g=9.8m/s2
- θ=19.8°
v=√100×9.8×tan(19.8°)
First, calculate tan(19.8°):
tan(19.8°)≈0.361
Now substitute:
v=√100×9.8×0.361
Calculating this gives:
v=√353.378≈18.7m/s
The speed of the train is approximately 18.7m/s.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (LONG ANSWER QUESTIONS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (FROM CENTRIPETAL FORCE)
31 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
A pendulum suspended from the ceiling of the train has a time period of two seconds when the train is at rest, then the time period of the pendulum, if the train accelerates 10 m/s2 will be (g=10m/s2)
View SolutionIn the Bohr model of hydrogen atom, the electron is treated as a particle going in a circle with the centre at the proton. The proton itself is assumed to be fixed in an inertial frame. The centripetal force is provided by the Coloumb attraction. In the ground state, the electron goes round the proton in a circle of radius 5.3×10−11m. Find the speed of the electron in the ground state. Mass of the electron =9.1×10−31kg and charge of the electron =1.6×10−19C.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by the string of the pendulum with the vertical if this angle does not change during the turn. Take g=10ms2.
View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
View SolutionA whistling train approaches a junction. An observer standing at juction observes the frequency to be 2.2KHz and 1.8KHz of the approaching and the receding train respectively. Find the speed of the train (speed of sound 300m/s)
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionA wagon of mass M can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass m is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle α from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
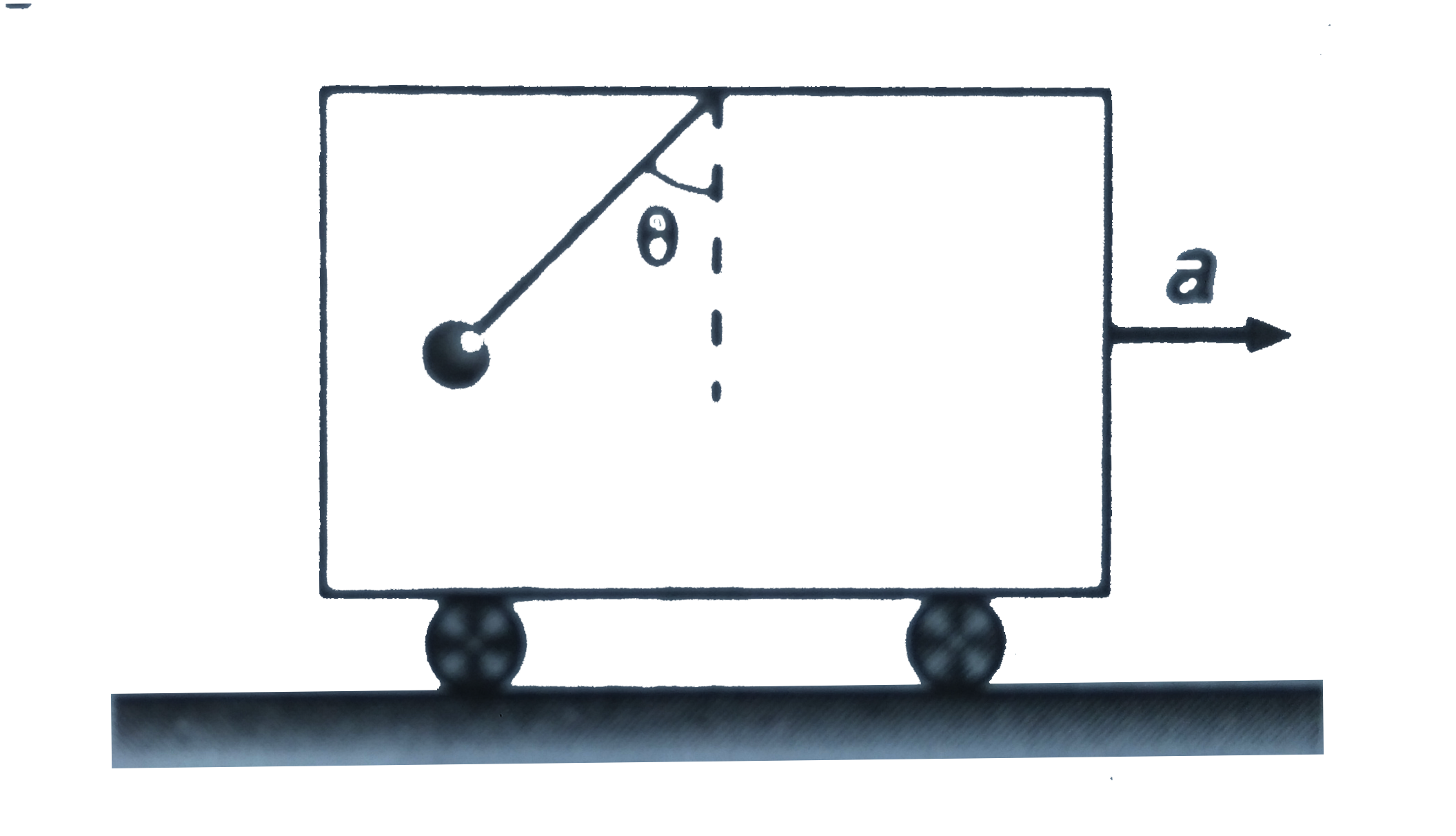
View Solution
