A train is moving with a speed of 20 m/s at a place where the radius of curvature of the railway line is 1500 m. Calculate the distance between the rails if the elevation of the outer rail above the inner rail is 0.042 m ?
The correct Answer is:1.54 m
To solve the problem, we need to find the distance between the rails (L) given the speed of the train (v), the radius of curvature (R), and the elevation of the outer rail above the inner rail (h).
1. Identify the Given Values:
- Speed of the train, v=20m/s
- Radius of curvature, R=1500m
- Elevation of the outer rail above the inner rail, h=0.042m
2. Use the Relationship Between Elevation and Distance:
We can use the formula derived from circular motion that relates the angle of elevation (θ), the height (h), and the distance between the rails (L):
tan2θ=v2gR
where g is the acceleration due to gravity (approximately 9.8m/s2).
3. Relate the Tangent to Height and Length:
From the geometry of the situation, we can express the tangent of the angle as:
tanθ=hL
4. Combine the Two Equations:
From the two equations, we can set them equal to each other:
hL=√v2gR
Rearranging gives:
L=h⋅gRv2
5. Substitute the Known Values:
Now, we can substitute the known values into the equation:
L=0.042⋅9.8⋅1500202
6. Calculate the Distance:
First, calculate the numerator:
0.042⋅9.8⋅1500=617.4
Then calculate the denominator:
202=400
Now divide:
L=617.4400=1.5435m
7. Round the Result:
Rounding to two decimal places, we find:
L≈1.54m
Final Answer:
The distance between the rails is approximately 1.54 meters.
- Speed of the train, v=20m/s
- Radius of curvature, R=1500m
- Elevation of the outer rail above the inner rail, h=0.042m
We can use the formula derived from circular motion that relates the angle of elevation (θ), the height (h), and the distance between the rails (L):
tan2θ=v2gR
where g is the acceleration due to gravity (approximately 9.8m/s2).
From the geometry of the situation, we can express the tangent of the angle as:
tanθ=hL
From the two equations, we can set them equal to each other:
hL=√v2gR
Rearranging gives:
L=h⋅gRv2
Now, we can substitute the known values into the equation:
L=0.042⋅9.8⋅1500202
First, calculate the numerator:
0.042⋅9.8⋅1500=617.4
Then calculate the denominator:
202=400
Now divide:
L=617.4400=1.5435m
Rounding to two decimal places, we find:
L≈1.54m
The distance between the rails is approximately 1.54 meters.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (LONG ANSWER QUESTIONS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM CENTRIPETAL FORCE)
Explore 31 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
A train is running at 20 m/s on a railway line with radius of curvature 40,000 metres. The distance between the two rails is 1.5 metres. For safe running of train the elevation of outer rail over the inner rail is (g=10m/s2)
View SolutionA point sourcs S is moving with a speed of 10m/s in x−y plane as shown in the figure. The radius of curvature of the concave mirror is 4m. Determine the velocity vector of the image formed by paraxial rays.
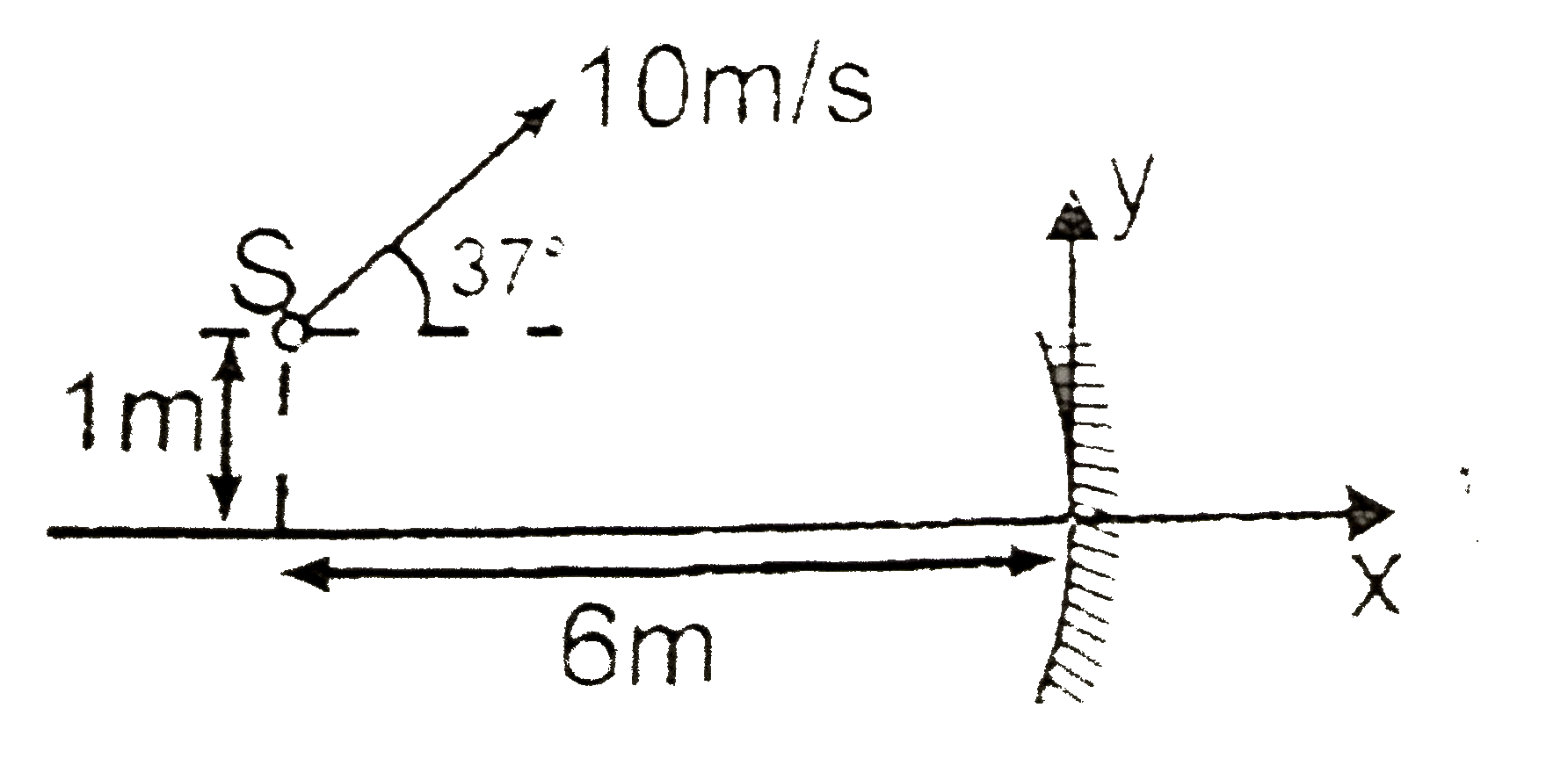
View SolutionA train has to negotiate a curve of 40 m radius. What is the super elevation of the outer rail required for a speed of 54kmh−1. The distance between the rails is one metre ?
View SolutionA broad gauge train runs at a speed of 72 km/h on a curved track of radius of curvature 1 km. Find the elevation of the outer rail above the inner rail so that there may be side-pressure on the rails ? Distance between the rails is 1.7 m.
View SolutionA railway track is banked for a speed v, by making the height of the outer rail h higher than that of the inner rail. The distance between the rails is d. The radius of curvature of the track is r
View SolutionCalculate the safe speed with which a train can negotiate a curve of 50 m radius, where the superelevation of the outer rail above the inner rail is 0.6 m. Given that the distance between the rails is 1 m
View SolutionA train moving with a velocity of 20 m s−1' is brought to rest by applying brakes in 5 s. Calculate the retardation.
View SolutionA car is moving towards south with a speed of 20ms−1. A motorcycst is moving towards east with a speed of 15ms−1. At a crttain instant, the motorcyclistis due south of the car and is at a distance of 50mfrom the car.
The shortest distance between the motorcyclist and the car is.
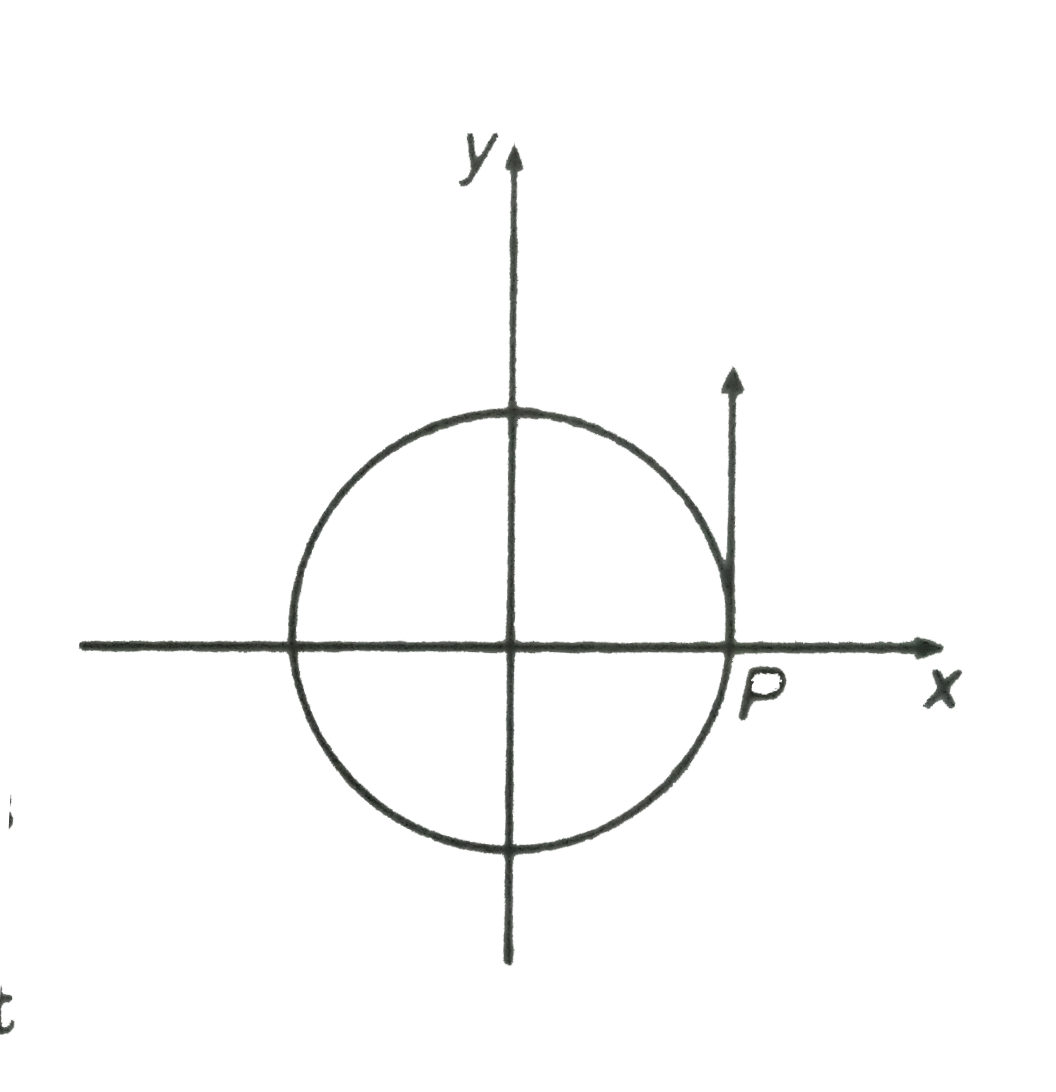
View SolutionA train is moving with a constant speed of 10m/s in a circle of radius 16πm. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed 10m/s relative to train towards negative x-axis at an angle of 37∘ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g =10m/s2,sin37∘=35
View SolutionA 210 meter long train is moving due north at a of 25 m/s. a small bird is flying due south a little above the train with speed 5 m/s. The time taken by the bird to cross the train is
View Solution

