A cyclist wants to loop a loop inside a death globe of radius 5 m. Calculate the least velocity the cyclist should have at the lowest point and calculate the height from which he should start ?
The correct Answer is:15.65ms−1
To solve the problem, we need to calculate the least velocity the cyclist should have at the lowest point of the loop and the height from which he should start.
Step 1: Calculate the minimum velocity at the lowest point
The minimum velocity v required at the lowest point of the loop can be derived from the condition that the centripetal force must be equal to the gravitational force acting on the cyclist at the top of the loop.
At the top of the loop, the gravitational force provides the necessary centripetal force. The formula for centripetal force is:
Fc=mv2r
Where:
- m is the mass of the cyclist,
- v is the velocity at the top of the loop,
- r is the radius of the loop.
At the top of the loop, the gravitational force mg must equal the centripetal force:
mg=mv2r
Cancelling m from both sides (assuming m≠0) gives:
g=v2r
Rearranging this equation to find v:
v=√gr
Given that the radius r=5 m and g≈9.8 m/s², we can substitute these values into the equation:
v=√9.8×5
Calculating this gives:
v=√49=7 m/s
Step 2: Calculate the height from which the cyclist should start
To find the height h from which the cyclist should start, we can use the principle of conservation of energy. The potential energy at the height h will be converted into kinetic energy at the lowest point of the loop.
The potential energy at height h is given by:
PE=mgh
The kinetic energy at the lowest point is given by:
KE=12mv2
Setting the potential energy equal to the kinetic energy:
mgh=12mv2
Cancelling m from both sides (assuming m≠0) gives:
gh=12v2
Rearranging to find h:
h=v22g
Substituting v=7 m/s and g=9.8 m/s²:
h=722×9.8
Calculating this gives:
h=4919.6≈2.5 m
Final Results
- The least velocity the cyclist should have at the lowest point is 7 m/s.
- The height from which he should start is approximately 2.5 m.
- m is the mass of the cyclist,
- v is the velocity at the top of the loop,
- r is the radius of the loop.
- The height from which he should start is approximately 2.5 m.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (LONG ANSWER QUESTIONS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM CENTRIPETAL FORCE)
Explore 31 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
As shown in the figure, a small is released from a certain height h which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
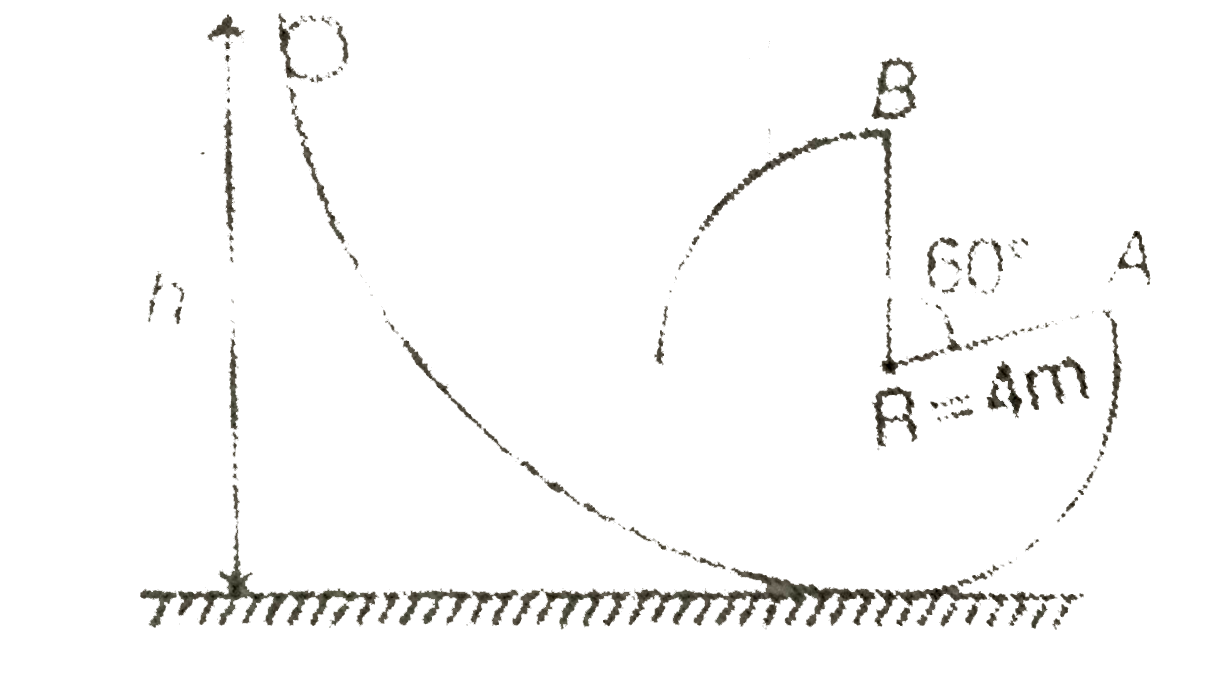
View SolutionAssertion For looping a verticla loop of radius, r the minimum velocity at lowest point should be √5gr. Reason In this event the velocityh at the highest point will be zero.
View Solution
Knowledge Check
A bubble having surface tension T and radius R is formed on a ring of radius b(b<<R). Air is blown inside the tube with velocity v as shown. The air molecule collides perpendicularly with the wall of the bubble and stops. Calculate the radius at which the bubble separates from the ring.
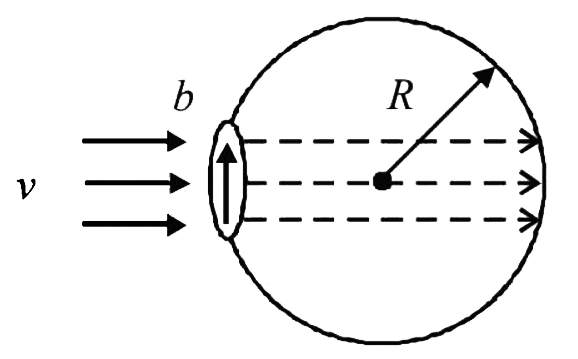 A1. 2Tρv2B2. 2TρvC3. 4Tρv2D4. 4Tρv
A1. 2Tρv2B2. 2TρvC3. 4Tρv2D4. 4Tρv
An object describes 225 m in the first 3s and 400 m in the next 2s.Calculate the velocity after 5s.From the start.
View SolutionAn object is thrown vertically upwards and rises to a height of 10 m. Calculate
(i) the velocity with which the object was thrown upwards and (ii) the time taken by the object to reach the highest point.
View SolutionA balloon starts ascending from the ground at a constant speed of 25m/s. After 5 s, a bullet is shot vertically upwards from the ground.
(i) What should be the minimun speed of the bullet so that it may reach the balloon?
(ii) The bullet is shot at twise the speed calculated in (i). Find the height at which it passes the balloon.
View SolutionIn order to get a billiard ball to roll without sliding from the start, where should the cue hit ? Calculate the height from centre of the sphere. Take R as the radius of sphere.
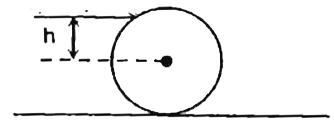
View SolutionA cyclist starts from the centre O of circular path of radius 10 m, covers the radius of circular path and reaches at point X on circumference, then cycles along the semi-circular path and reaches the point Y. If he takes 10 minutes to go from O to Y via X, then the net displacement and average speed of the cyclist would be
View SolutionA cabin is moving upwards with a constant acceleration g. A boy standing in the cabin wants to whirl a particle of mass m in a vertical circle of radius l. (Mass is attached to an ideal string.) Calculate minimum velocity which should be provided at lowermost point (w.r.t cabin) so that particle can just complete the circle.
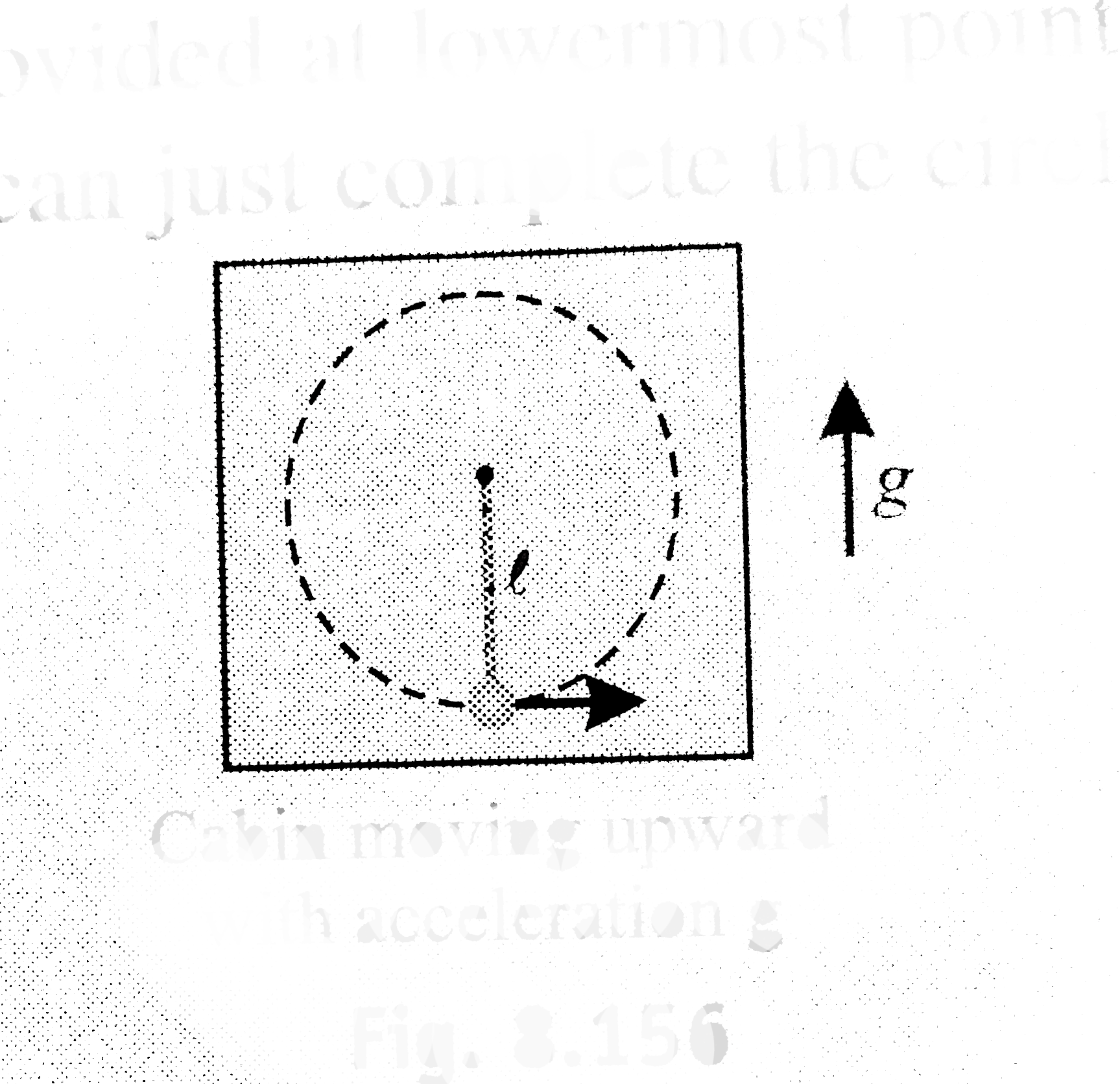
View SolutionA sphere of radius 0.1m and mass 8πkg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
View Solution

