In the Atwood's machine shown in Fig. m1=7 kg and m2=12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley of radius 5 cm. When the system is released from rest the heavier mass is found to fall 1 m in 2 s. Calculate the moment of inertia of the pulley ?
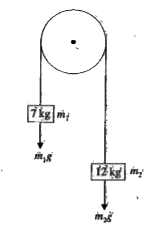
m1=7kg,m2=12kg
Radius of the pulley =r=5cm=0.05 m
Moment of intertia of the pulley = l = ?
Displacement of the block =s =1 m
Time =t =2s
Linear acceleration a= ?
s=ut+12at2
a=2st22×122=0.5m/s2
Decrease in P.E. of the system = Increase in K.E. of the system
(m2gs~m1s)=12m1v21+12m2v2+12Iω2
v21=v22=2as
Final angular velocity of the pulley ω=ω0+αl=0+art
m2gs−m1gs=12m1×2as+12m2×2as+12I×a2t2r2
(m2−m1)gs=(m1+m2)as+Ia2t22r2
I=[(m2−m1)gs−(m1+m2)as]=2r2a2t2
=[(12−7)9.8×1−(12+7)×0.5×1]×2×0.020.52×22=3.95kgm2
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
11 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley. Find the acceleration of the masses and tension in the string , when the masses are released
 .
.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View Solution
Knowledge Check
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley Find the acceleration of the masses and tension in the string , when the masses are released
 . Ag4Bg5Cg8Dg6
. Ag4Bg5Cg8Dg6
Two masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
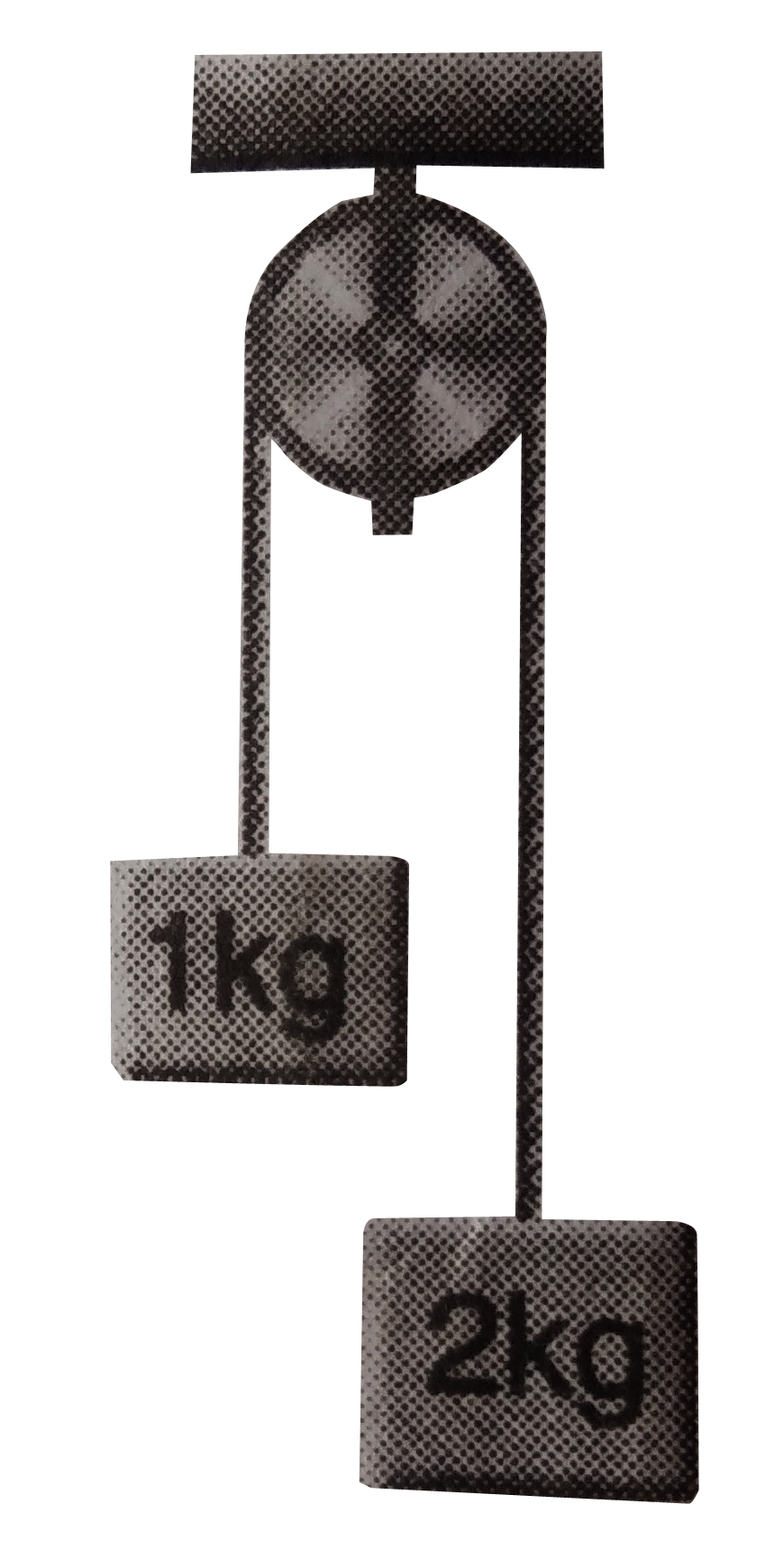
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
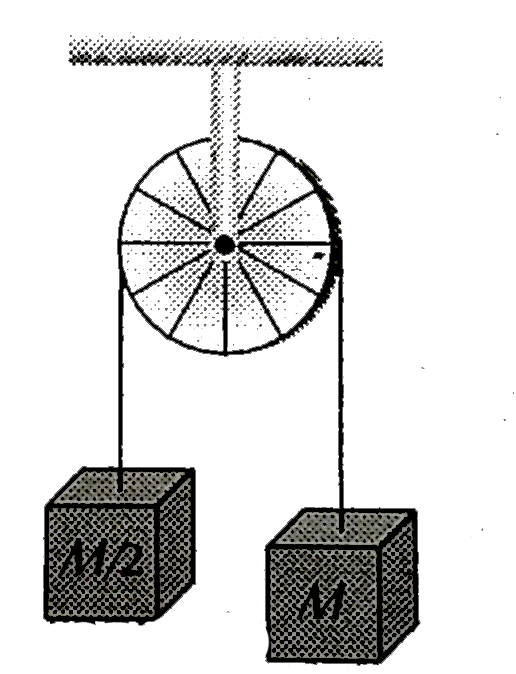
View SolutionTwo masses M1=5kg, M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
(a) g (b) g2 (c) g3 (d) g4

View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)

View Solution
