Three masses 3, 4 and 5 kg are placed at the centre of an equiliteral triangle of 1 m sides. Locate its centre of mass.
To locate the center of mass of the three masses (3 kg, 4 kg, and 5 kg) placed at the vertices of an equilateral triangle with side length of 1 meter, we can follow these steps:
1. Identify the Coordinates of the Masses:
- Place the triangle in a coordinate system. Let the vertices of the equilateral triangle be:
- Mass M1 (3 kg) at A (0, 0)
- Mass M2 (4 kg) at B (1, 0)
- Mass M3 (5 kg) at C (0.5, √32) (This is the height of the triangle).
2. Calculate the Total Mass:
- Total mass M=M1+M2+M3=3+4+5=12 kg.
3. Calculate the x-coordinate of the Center of Mass (x_cm):
- The formula for the x-coordinate of the center of mass is:
xcm=M1⋅x1+M2⋅x2+M3⋅x3M
- Substituting the values:
xcm=(3⋅0)+(4⋅1)+(5⋅0.5)12
xcm=0+4+2.512=6.512=0.54 m
4. Calculate the y-coordinate of the Center of Mass (y_cm):
- The formula for the y-coordinate of the center of mass is:
ycm=M1⋅y1+M2⋅y2+M3⋅y3M
- Substituting the values:
ycm=(3⋅0)+(4⋅0)+(5⋅√32)12
ycm=0+0+5√3212=5√324≈0.36 m
5. Conclusion:
- The center of mass of the system is located at:
(xcm,ycm)=(0.54 m,0.36 m)
- Place the triangle in a coordinate system. Let the vertices of the equilateral triangle be:
- Mass M1 (3 kg) at A (0, 0)
- Mass M2 (4 kg) at B (1, 0)
- Mass M3 (5 kg) at C (0.5, √32) (This is the height of the triangle).
- Total mass M=M1+M2+M3=3+4+5=12 kg.
- The formula for the x-coordinate of the center of mass is:
xcm=M1⋅x1+M2⋅x2+M3⋅x3M
- Substituting the values:
xcm=(3⋅0)+(4⋅1)+(5⋅0.5)12
xcm=0+4+2.512=6.512=0.54 m
- The formula for the y-coordinate of the center of mass is:
ycm=M1⋅y1+M2⋅y2+M3⋅y3M
- Substituting the values:
ycm=(3⋅0)+(4⋅0)+(5⋅√32)12
ycm=0+0+5√3212=5√324≈0.36 m
- The center of mass of the system is located at:
(xcm,ycm)=(0.54 m,0.36 m)
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
Explore 11 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (LONG ANSWER QUESTIONS)
Explore 8 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
The position co-ordinates of the centre of mass of a system of three particles of equal masses which are placed on the verctices of an equilateral triangle of a side a are shown. Locate centre mass?

View SolutionThree masses of 1kg, 2kg, and 3kg, are placed at the vertices of an equilateral triangle of side 1m. Find the gravitational potential energy of this system.
Take G=6.67×10−11N−m2/kg2.
View SolutionThree masses of 2 kg, 3 kg and 4 kg are located at the three vertices of an equilateral triangle of side 1 m. What is the M.I. of the system about an axis along the altitude of the triangle and passing through the 3 kg mass?
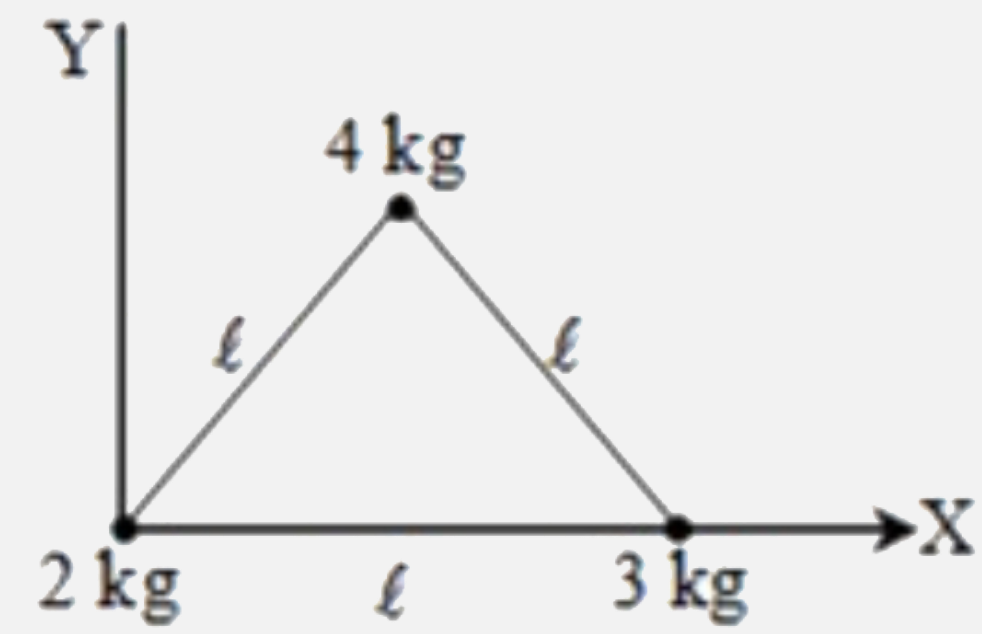
View SolutionThree masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
View SolutionThree masses of 1kg, 2kg, and 3kg, are placed at the vertices of an equilateral triangle of side 1m. Find the gravitational potential energy of this system.
Take G=6.67×10−11N−m2/kg2.
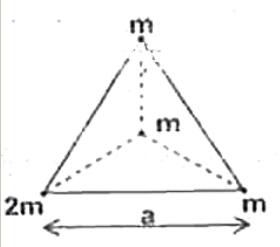
View SolutionThree point masses m,m and 2m are placed on the vertex of an equilateral triangle of side 'a' Another point mass 'm' is placed at the centroid of the triangle as shown in the figure. If the magnitude of net force on the point mass placed at centroid is KGm2a2 then find the value of K (G= universal gravitational constant )
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
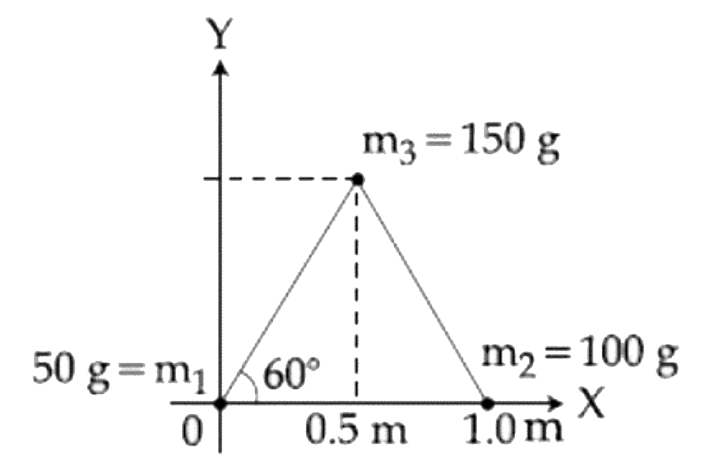
View SolutionThree particles of massses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side 1m ( as shown in the figure ) . The ( x, y) coordinates of the centre of mass will be :
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral triangle of side 1. What is the gravitational field and potential due to the three masses at the centroid of the triangle ?
View SolutionThree balls of masses 1kg,2kgand3kg are arranged at the corners of an equilateral triangle of side 1m. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View Solution

