A flywheel requires 3 s to rotate through 234 radian. If its angular velocity at 3 s is 108 rad/s, find the initial velocity and uniform acceleration.
To solve the problem step by step, we will use the formulas related to angular motion.
Step 1: Identify the given values
- Angular displacement (θ) = 234 radians
- Time (t) = 3 seconds
- Final angular velocity (ω) at t = 3 seconds = 108 rad/s
Step 2: Use the formula for angular displacement
The formula for angular displacement when angular acceleration is uniform is:
θ=(ω+ω0)2⋅t
where:
- θ is the angular displacement,
- ω is the final angular velocity,
- ω₀ is the initial angular velocity,
- t is the time.
Step 3: Substitute the known values into the formula
We can rearrange the formula to solve for the initial angular velocity (ω₀):
234=(108+ω0)2⋅3
Step 4: Simplify the equation
Multiply both sides by 2 to eliminate the fraction:
468=(108+ω0)⋅3
Now, divide both sides by 3:
156=108+ω0
Step 5: Solve for initial angular velocity (ω₀)
Subtract 108 from both sides:
ω0=156−108=48 rad/s
Step 6: Find the angular acceleration (α)
We can use the formula for angular acceleration:
α=ω−ω0t
Substituting the known values:
α=108−483
Step 7: Simplify the calculation
α=603=20 rad/s2
Final Results
- Initial angular velocity (ω₀) = 48 rad/s
- Angular acceleration (α) = 20 rad/s²
- Angular displacement (θ) = 234 radians
- Time (t) = 3 seconds
- Final angular velocity (ω) at t = 3 seconds = 108 rad/s
The formula for angular displacement when angular acceleration is uniform is:
θ=(ω+ω0)2⋅t
where:
- θ is the angular displacement,
- ω is the final angular velocity,
- ω₀ is the initial angular velocity,
- t is the time.
We can rearrange the formula to solve for the initial angular velocity (ω₀):
234=(108+ω0)2⋅3
Multiply both sides by 2 to eliminate the fraction:
468=(108+ω0)⋅3
Now, divide both sides by 3:
156=108+ω0
Subtract 108 from both sides:
ω0=156−108=48 rad/s
We can use the formula for angular acceleration:
α=ω−ω0t
Substituting the known values:
α=108−483
α=603=20 rad/s2
- Initial angular velocity (ω₀) = 48 rad/s
- Angular acceleration (α) = 20 rad/s²
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
11 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
If Sn=2+0.4n find initial velocity and acceleration
View SolutionA flywheel at rest is to reach an angular velocity of 24 rad/s in 8 second with constant angular acceleration. The total angle turned through during this interval is
View SolutionA wheel starts rotating at 10 rad/sec and attains the angular velocity of 100 rad/sec in 15 seconds. What is the angular acceleration in rad/sec2?
View SolutionA car travels a distance 100 m with a constant acceleration and average velocity of 20 m s−1 . The final velocity acquired by the car is 25 m s−1. Find : (i) the initial velocity and (ii) acceleration of car.
View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.
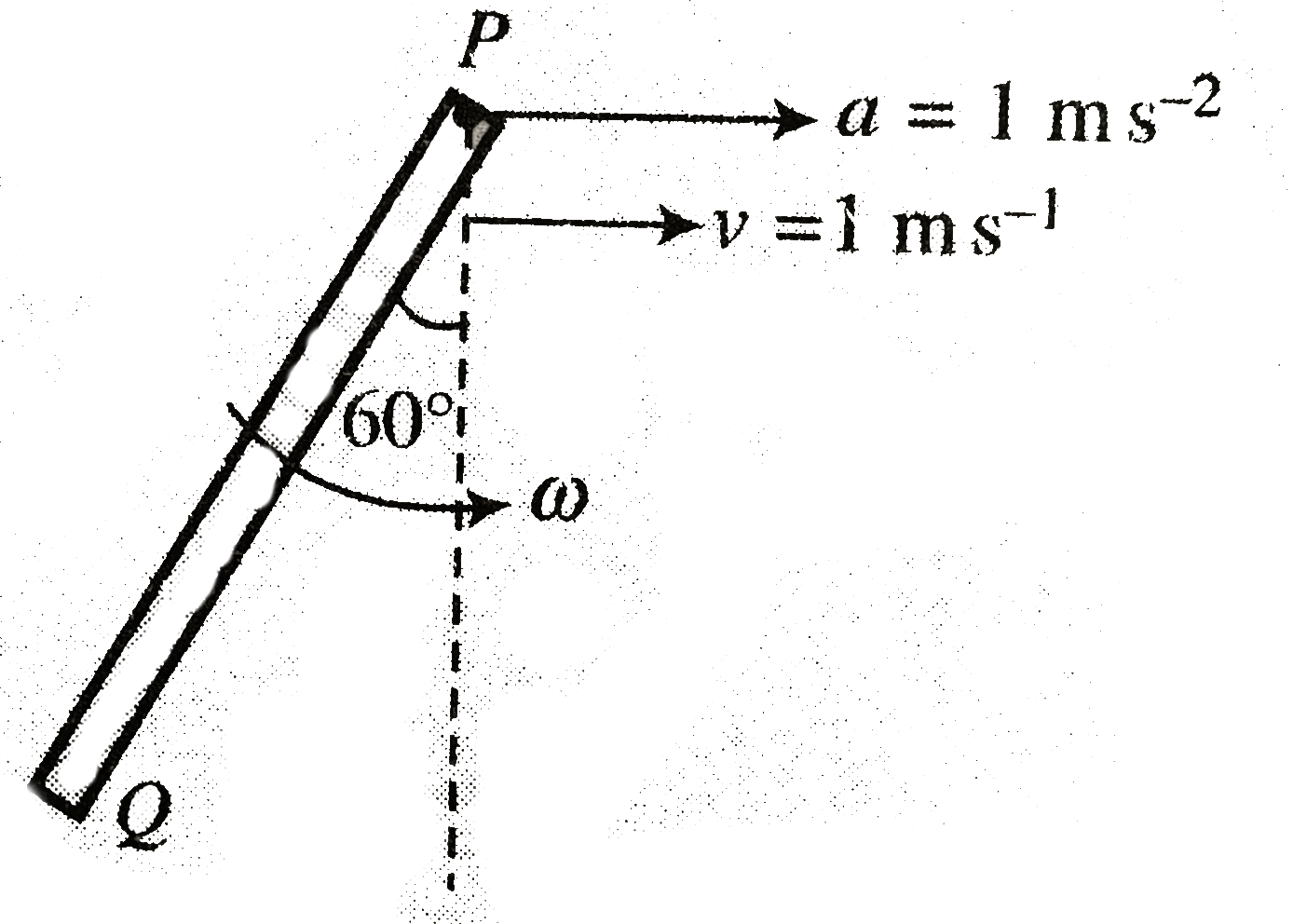
View SolutionA flywheel rotates with a uniform angular acceleration. Its angular velocity increases from 20πrad/s to 40πrad/s in 10 seconds. How many rotations did it make in this period ?
View SolutionIf a disc starting from rest acquires an angular velocity of 240rev min−1 in 10 s, then its angular acceleration will be
View SolutionA wheel is rotating with an angular velocity of 3rads−1. If the angular acceleration is 2rads−1 then calculate its angular velocity after 5 second.
View SolutionA wheel is rotating with an angular velocity of 3rads−1. If the angular acceleration is 2rads−1 then calculate its angular velocity after 5 second.
View SolutionThe initial angular velocity of a heavy flywheel rotating on its axis is w0. Its angular velocity decreases due to friction. At the end of the first minute its angular velocity is 0.8ω0. What is its angular velocity at the end of third minute, if the frictional force is constant ?
View Solution
