In ΔABCAD divides BC in 1 : 3 find the ratio of triangle ADB and ADC ?
The correct Answer is:1√6
To find the ratio of the areas of triangles ADB and ADC, we can follow these steps:
Step 1: Understand the problem
We have triangle ABC with point D on line segment BC such that AD divides BC in the ratio 1:3. This means that BD:DC = 1:3.
Step 2: Assign lengths to segments
Let the length of segment BD be x. Since BD:DC = 1:3, the length of segment DC will be 3x. Therefore, the total length of segment BC is:
BC=BD+DC=x+3x=4x
Step 3: Calculate the areas of triangles ADB and ADC
The area of a triangle can be calculated using the formula:
Area=12×base×height
- For triangle ADB:
- Base = BD = x
- Height = h (the perpendicular distance from A to line BC)
Thus, the area of triangle ADB is:
AreaADB=12×x×h
- For triangle ADC:
- Base = DC = 3x
- Height = h (the height remains the same since it is the same vertex A)
Thus, the area of triangle ADC is:
AreaADC=12×3x×h
Step 4: Find the ratio of the areas
Now, we can find the ratio of the areas of triangles ADB and ADC:
Ratio=AreaADBAreaADC=12×x×h12×3x×h
Step 5: Simplify the ratio
The 12 and h cancel out:
Ratio=x3x=13
Thus, the ratio of the areas of triangles ADB and ADC is:
Ratio of AreaADB:AreaADC=1:3
Final Answer:
The ratio of the areas of triangles ADB and ADC is 1:3.
---
We have triangle ABC with point D on line segment BC such that AD divides BC in the ratio 1:3. This means that BD:DC = 1:3.
Let the length of segment BD be x. Since BD:DC = 1:3, the length of segment DC will be 3x. Therefore, the total length of segment BC is:
BC=BD+DC=x+3x=4x
The area of a triangle can be calculated using the formula:
Area=12×base×height
- Base = BD = x
- Height = h (the perpendicular distance from A to line BC)
Thus, the area of triangle ADB is:
AreaADB=12×x×h
- Base = DC = 3x
- Height = h (the height remains the same since it is the same vertex A)
Thus, the area of triangle ADC is:
AreaADC=12×3x×h
Now, we can find the ratio of the areas of triangles ADB and ADC:
Ratio=AreaADBAreaADC=12×x×h12×3x×h
The 12 and h cancel out:
Ratio=x3x=13
Ratio of AreaADB:AreaADC=1:3
The ratio of the areas of triangles ADB and ADC is 1:3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let AD be a median of the ΔABC. If AE and AF are medians of the triangle ABD and ADC, respectively, and AD = m1,AE=m2,AF=m3, then a2/8 is equal to
Am22+m23−2m21Bm21+m22−2m23Cm21+m23−2m22Dnone of these
In ΔABC,AD=BC. Find x.
View SolutionIn a ΔABC,AD is a median. The bisectors of ∠ADBand∠ADC meets AB & AC at E and F respectively . AE:BE=3:4 . Find EF:BC.
View SolutionIn a ΔABC,DE∣∣BC AD : BD = 3 : 5 find the ratio of area of ADE to Quedrilateral BCED
View SolutionIn the given figure, if DE∣∣BC, then find the ratio of area of (△ADE) and (□DECB).
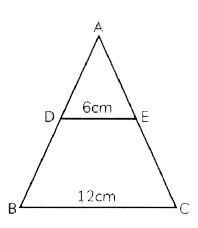
View SolutionIn triangle ABC, A=90∘andAB=3 unit, AC = 4 unit and side AD is perpendicular on BC then find the area of triangle ADB?
View SolutionΔABC is isosceles with AB=AC. Also. AD⊥BC meeting BC in D. Are the two triangles ABD and ACD congruent? State in symbolic form. Which congruence condition do you use? Which side of ADC equals BD? Which angle ofΔADC equals∠B?
View SolutionFind the ratio of area of ΔADE to Δ ABC

View Solution
