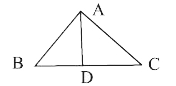
In A AB = 10 AC = 18 AD is angle bisector If area of is 28 . find area of ADB ?
The correct Answer is:45
To find the area of triangle ADB given the triangle ABC, where AB = 10, AC = 18, AD is the angle bisector, and the area of triangle ABC is 28, we can follow these steps:
1. Draw Triangle ABC:
- Sketch triangle ABC with vertices A, B, and C.
- Mark AB = 10 and AC = 18.
2. Identify the Angle Bisector:
- Draw the angle bisector AD from vertex A to side BC, intersecting at point D.
3. Use the Angle Bisector Theorem:
- According to the angle bisector theorem, the ratio of the lengths of the two segments created on side BC (BD and DC) is equal to the ratio of the lengths of the other two sides (AB and AC).
- Therefore, ABAC=BDDC.
- Substituting the known values:
1018=BDDC⟹59=BDDC
- Let BD = 5x and DC = 9x for some value x.
4. Calculate the Total Length of BC:
- The total length of BC is:
BD+DC=5x+9x=14x
5. Determine the Areas of Triangles ADB and ADC:
- The area of triangle ADB and triangle ADC will be in the same ratio as the lengths BD and DC.
- Therefore, the area of triangle ADB : area of triangle ADC = 5 : 9.
6. Set Up the Area Equation:
- Let the area of triangle ADB be 5k and the area of triangle ADC be 9k.
- The total area of triangle ABC is given as 28:
5k+9k=28⟹14k=28
7. Solve for k:
- Dividing both sides by 14:
k=2
8. Find the Area of Triangle ADB:
- Now, substitute k back to find the area of triangle ADB:
Area of ADB=5k=5×2=10 cm2
Final Answer:
The area of triangle ADB is 10 cm².
- Sketch triangle ABC with vertices A, B, and C.
- Mark AB = 10 and AC = 18.
- Draw the angle bisector AD from vertex A to side BC, intersecting at point D.
- According to the angle bisector theorem, the ratio of the lengths of the two segments created on side BC (BD and DC) is equal to the ratio of the lengths of the other two sides (AB and AC).
- Therefore, ABAC=BDDC.
- Substituting the known values:
1018=BDDC⟹59=BDDC
- Let BD = 5x and DC = 9x for some value x.
- The total length of BC is:
BD+DC=5x+9x=14x
- The area of triangle ADB and triangle ADC will be in the same ratio as the lengths BD and DC.
- Therefore, the area of triangle ADB : area of triangle ADC = 5 : 9.
- Let the area of triangle ADB be 5k and the area of triangle ADC be 9k.
- The total area of triangle ABC is given as 28:
5k+9k=28⟹14k=28
- Dividing both sides by 14:
k=2
- Now, substitute k back to find the area of triangle ADB:
Area of ADB=5k=5×2=10 cm2
The area of triangle ADB is 10 cm².
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a triangle ABC, AB = 8 cm, AC = 10 cm and ∠B=90∘, then the area of ΔABC is
A49 sq. cmB36 sq. cmC25 sq. cmD24 sq. cmIn a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49B49:25C6:1D5:7Let AD be the angle bisector of ∠A of ΔABC such that AD=αAB+βAC, then
Aα=|AB||AB|+|AC|,β=|AC||AB|+|AC|Bα=|AB|+|AC||AB|,β=|AB|+|AC||AC|Cα=|AC||AB|+|AC|,β=|AB||AB|+|AC|Dα=|AB||AC|,β=|AC||AB|
In a ΔABC,∠B=2∠C Angle bisector AD and BE intersect of O. AB = CD find ∠ABC
View SolutionIn a ΔABC,AB=12cm,∠ABC=30∘,∠ACB=45∘ find the area of ΔABC .
View SolutionIn ΔABC∠B=60∘∠C=45∘AB=12 cm Find area of Δ
View SolutionIn a ΔABC,∠A=120∘,AB=20cm,AC=30cm find the angle bisector AD .
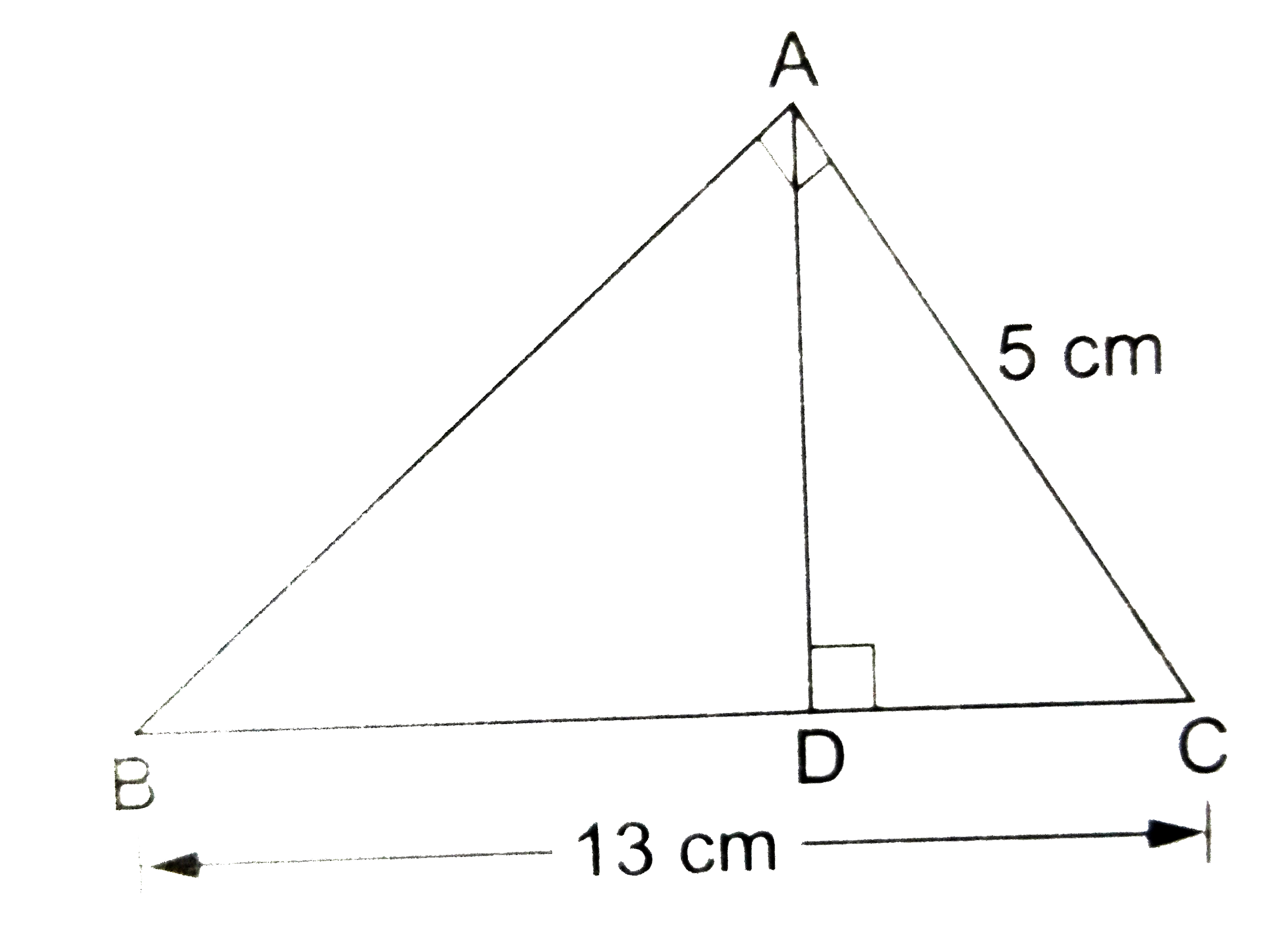
View SolutionΔABC is right-angled at A and AD⊥BC. If BC=13cmandAC=5cm, find the ratio of areas of ΔABCandΔADC.
View Solution