Question

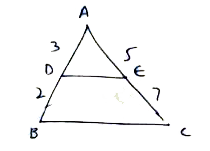
In a $\Delta ABC,DE\mid \mid BC$ AD : BD = 3 : 5 find the ratio of area of ADE to Quedrilateral BCED

Answer

`(9)/(55)`

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Given Ratios
We are given that in triangle ABC, line DE is parallel to line BC, and the ratio of AD to BD is 3:5. This means:
- AD = 3 parts
- BD = 5 parts

Step 2: Find the Length of AB
Since AD and BD are parts of AB, we can find the total length of AB:
\( AB = AD + BD = 3 + 5 = 8 \)

Step 3: Establish the Ratio of Similar Triangles
Since DE is parallel to BC, triangles ADE and ABC are similar. The ratio of the corresponding sides of similar triangles is equal to the ratio of their areas. Therefore, we can express the ratio of the sides as follows:
\( \frac{AD}{AB} = \frac{3}{8} \)

Step 4: Calculate the Ratio of Areas
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides:
\( \text{Area Ratio} = \left(\frac{AD}{AB}\right)^2 = \left(\frac{3}{8}\right)^2 = \frac{9}{64} \)

This means:
- Area of triangle ADE = 9 parts
- Area of triangle ABC = 64 parts

Step 5: Find the Area of Quadrilateral BCED
To find the area of quadrilateral BCED, we subtract the area of triangle ADE from the area of triangle ABC:
\( \text{Area of quadrilateral BCED} = \text{Area of triangle ABC} - \text{Area of triangle ADE} \)
\( = 64 - 9 = 55 \)

Step 6: Find the Ratio of Areas of ADE to BCED
Now, we can find the ratio of the area of triangle ADE to the area of quadrilateral BCED:
\( \text{Ratio} = \frac{\text{Area of triangle ADE}}{\text{Area of quadrilateral BCED}} = \frac{9}{55} \)

Thus, the final answer is:
The ratio of the area of triangle ADE to the area of quadrilateral BCED is 9:55.

---