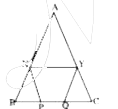
In a equilateral ΔABC having sides 30cmXY||BC,XP||AX,YQ∣∣AB
XY + xP + YQ = 40 cm find PQ
The correct Answer is:PQ=10cm
To solve the problem step by step, we will analyze the given information about the equilateral triangle ABC and the parallel lines XY, XP, and YQ.
1. Draw the Equilateral Triangle:
- Draw triangle ABC with sides AB = BC = CA = 30 cm.
- Mark points X and Y on sides AB and AC respectively, such that line XY is parallel to side BC.
2. Identify Relationships:
- Since XY is parallel to BC, triangles BXP and CXY are similar to triangle ABC.
- Similarly, YQ is parallel to AB, which means triangles CYQ and ABY are also similar.
3. Use the Given Information:
- We know that XY+XP+YQ=40cm.
- Let’s denote XP=BX and YQ=CY.
4. Express the Lengths:
- Since triangle ABC is equilateral, we have:
- BC=BP+PC
- BP=BX and CQ=CY
- Therefore, we can write:
- BC=BX+PQ+CY
5. Substitute Known Values:
- We know BC=30cm.
- From the previous steps, we can substitute BX and CY into the equation:
- 30=BX+PQ+CY
6. Relate to the Given Sum:
- From the equation XY+BX+CY=40:
- We can express CY as YQ.
- Rearranging gives us:
- YQ+BX=40−XY
7. Calculate YQ:
- Since YQ=CY, we can substitute CY back into the equation:
- 30=BX+PQ+YQ
- We can express YQ in terms of BX:
- YQ=40−XY−BX
8. Substituting Values:
- Assume XY=10cm (as derived from the earlier steps):
- Thus, YQ=10cm (since YQ=CY).
- Substitute YQ back into the equation:
- 30=BX+PQ+10
9. Solve for PQ:
- Rearranging gives:
- PQ=30−BX−10
- Since BX=10cm:
- PQ=30−10−10=10cm.
Final Answer:
- The length of PQ is 10cm.
- Draw triangle ABC with sides AB = BC = CA = 30 cm.
- Mark points X and Y on sides AB and AC respectively, such that line XY is parallel to side BC.
- Since XY is parallel to BC, triangles BXP and CXY are similar to triangle ABC.
- Similarly, YQ is parallel to AB, which means triangles CYQ and ABY are also similar.
- We know that XY+XP+YQ=40cm.
- Let’s denote XP=BX and YQ=CY.
- Since triangle ABC is equilateral, we have:
- BC=BP+PC
- BP=BX and CQ=CY
- Therefore, we can write:
- BC=BX+PQ+CY
- We know BC=30cm.
- From the previous steps, we can substitute BX and CY into the equation:
- 30=BX+PQ+CY
- From the equation XY+BX+CY=40:
- We can express CY as YQ.
- Rearranging gives us:
- YQ+BX=40−XY
- Since YQ=CY, we can substitute CY back into the equation:
- 30=BX+PQ+YQ
- We can express YQ in terms of BX:
- YQ=40−XY−BX
- Assume XY=10cm (as derived from the earlier steps):
- Thus, YQ=10cm (since YQ=CY).
- Substitute YQ back into the equation:
- 30=BX+PQ+10
- Rearranging gives:
- PQ=30−BX−10
- Since BX=10cm:
- PQ=30−10−10=10cm.
- The length of PQ is 10cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A sum of Rs. 4,300 is distributed among M, N and O, such that M receives 25% more than N and N receives 25% less than O. What is O’s share in the amount?
AA) 1564BB) 1600CC) 1632DD) 1714
Find the area of an equilateral triangle having each side 4cm.
In equilateral triangle ABC, AB=BC=AC=a
s=12(a+a+a)
=32a
now, ar△ABC=√32a(32a−a)(32a−a)(32a−a)
⇒√32a×a2×a2×a2
⇒√(a2)4×3
⇒a2√34
View SolutionFind the area of an equilateral triangle having each side 4 cm.
View SolutionThe given figure shows an equilateral triangle ABC with each side 15 cm. Also DE||BC,DF||AC,EG∣∣AB If DE + DF + EG = 20 cm, find FG.
View SolutionABC is a triangle ,and XY is drawn parallel to BC cutting AB at X and AC at Y .
If AB = 12 cm , AC = 9 cm , and AY = 5.4 cm , find BX .
View SolutionTriangles PQR and ABC are similar triangles. Triangle ABC have the following sides AB = 36 cm AC = 20 cm CB = 48 cm, Triangle PQR have the following sides: PQ = 9 cm PR = 5 cm What is the length of side RQ=?
View SolutionIn the figure given below, ABC is an equilateral triangle with each side of length 30 cm. XY is parallel to BC, XP is parallel to AC and YQ is parallel to AB. If XY + XP + YQ is 40 cm, then the value of PQ is
View SolutionABC is a triangle ,and XY is drawn parallel to BC cutting AB at X and AC at Y .
If AX = 5.6 cm , XB = 1.6 cm , and AY = 8.4 cm , find AC.
View Solution