Find the ratio of AD and CD when AB = 3 cm BC = 4 cm ∠B=90∘. Also find area of ΔADB
The correct Answer is:5425cm2
To solve the problem, we need to find the ratio of AD and CD in triangle ABC, where AB = 3 cm, BC = 4 cm, and angle B = 90 degrees. We also need to find the area of triangle ADB.
Step 1: Identify the triangle and its sides
We have a right triangle ABC with:
- AB = 3 cm (one leg)
- BC = 4 cm (the other leg)
- Angle B = 90 degrees
Step 2: Calculate the hypotenuse AC using the Pythagorean theorem
Using the Pythagorean theorem:
AC=√AB2+BC2=√32+42=√9+16=√25=5 cm
Step 3: Draw the perpendicular line BD
We draw a perpendicular line from B to AC, meeting at point D. This creates two segments AD and CD.
Step 4: Calculate lengths AD and CD
Using the formulas for the segments in a right triangle:
AD=AB2AC=325=95 cm
CD=BC2AC=425=165 cm
Step 5: Find the ratio of AD to CD
Now, we can find the ratio of AD to CD:
Ratio of AD to CD=ADCD=95165=916
Step 6: Calculate the length of BD
Using the formula for BD:
BD=AB×BCAC=3×45=125 cm
Step 7: Calculate the area of triangle ADB
The area of triangle ADB can be calculated using the formula for the area of a triangle:
Area=12×base×height
Here, the base is BD and the height is AD:
Area of ΔADB=12×BD×AD=12×125×95=12×10825=5425 cm2
Final Answers
- The ratio of AD to CD is 916.
- The area of triangle ADB is 5425 cm2.
We have a right triangle ABC with:
- AB = 3 cm (one leg)
- BC = 4 cm (the other leg)
- Angle B = 90 degrees
Using the Pythagorean theorem:
AC=√AB2+BC2=√32+42=√9+16=√25=5 cm
We draw a perpendicular line from B to AC, meeting at point D. This creates two segments AD and CD.
Using the formulas for the segments in a right triangle:
AD=AB2AC=325=95 cm
CD=BC2AC=425=165 cm
Now, we can find the ratio of AD to CD:
Ratio of AD to CD=ADCD=95165=916
Using the formula for BD:
BD=AB×BCAC=3×45=125 cm
The area of triangle ADB can be calculated using the formula for the area of a triangle:
Area=12×base×height
Here, the base is BD and the height is AD:
Area of ΔADB=12×BD×AD=12×125×95=12×10825=5425 cm2
- The ratio of AD to CD is 916.
- The area of triangle ADB is 5425 cm2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A park is in the shape of quadrilateral ABCD in which AB=9cm,BC=12cm,CD=5cm,AD=8cm and ∠C=90∘. Find the area of the park.
A65.4cm2B69.4cm2C66.4cm2D68.4cm2In the given figure, AB⊥AD,BC⊥BD and AD = 9 cm, BC = 8 cm and CD= 17 cm. Find the area of quadrilateral ABCD
 A112 cm2B114 cm2C119 cm2D117 cm2
A112 cm2B114 cm2C119 cm2D117 cm2In the given figure AD=15cm,AB=20cmandBC=CD=25cm. Find the area of □ABCD:
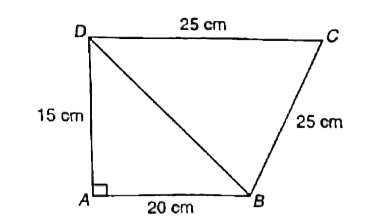 A254(24+25√3)cm2B24(25+24√3)cm2C252(24+25√3)cm2Dnone of these
A254(24+25√3)cm2B24(25+24√3)cm2C252(24+25√3)cm2Dnone of these
In the given quadrilateral ABCD,AB=15cm,BC=20cmandAD=7cm∠ABC=∠ADC=90∘. Find the length of side CD:
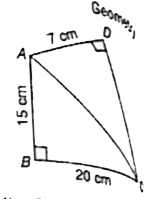
View SolutionFind the perimeter and area of the quadrilateral ABCD in which AB= 17 cm AD=9cm,CD=12cm∠ACB=90∘ and AC=15 cm.
View Solution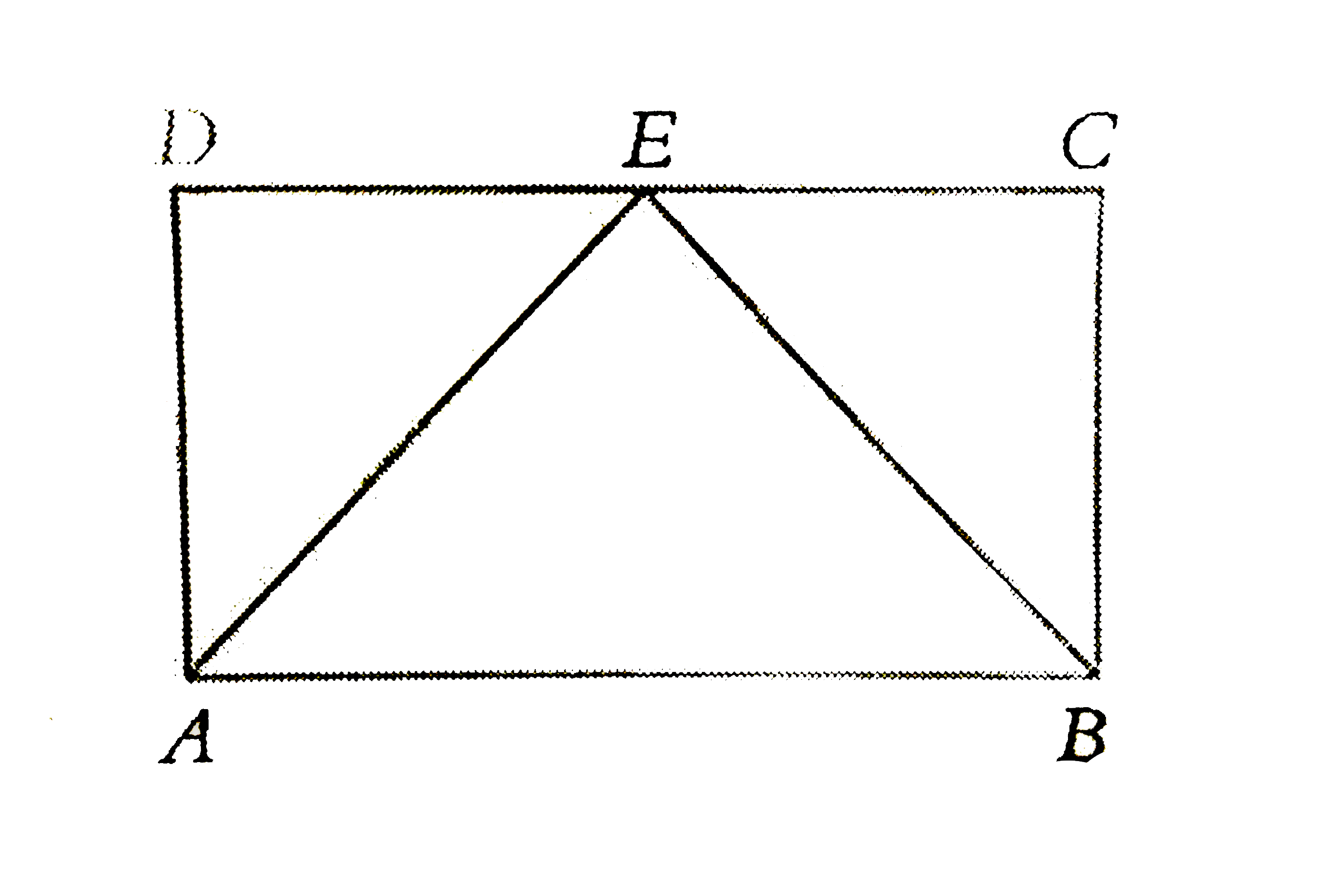
In the figure above ( not to scale ), ABCD is a rectangle, E is the mid - point of CD. If CD=24 cm and AD=5 cm, then find the perimeter of ΔABE.
View SolutionIn a ΔABC, angle bisector of interior angle A meets BC at D . if AB = 25 cm & AC = 20 cm If length of CD = 16 cm find length of BC ?
View SolutionIn the figure ∠ADC=90∘,BC=38cm,CD=28cmandBP=25cm
Find the radius of the circle.
View Solution