ABC is an isosceles right angle . If Perimeter is P find Area
The correct Answer is:
To find the area of an isosceles right triangle ABC with a given perimeter P, we can follow these steps:
Step 1: Understand the triangle properties
An isosceles right triangle has two equal sides and a right angle (90 degrees) between them. Let's denote the lengths of the equal sides as a and the hypotenuse as AC.
Step 2: Express the perimeter
The perimeter P of triangle ABC can be expressed as:
P=AB+BC+AC=a+a+AC=2a+AC
Step 3: Use the Pythagorean theorem
According to the Pythagorean theorem:
AC2=AB2+BC2
Since AB=a and BC=a:
AC2=a2+a2=2a2
Thus, we can find AC:
AC=√2a2=a√2
Step 4: Substitute AC into the perimeter equation
Now substitute AC back into the perimeter equation:
P=2a+a√2
This can be rearranged to find a:
P=a(2+√2)
So,
a=P2+√2
Step 5: Rationalize the expression for a
To simplify a, we can rationalize the denominator:
a=P(2−√2)(2+√2)(2−√2)=P(2−√2)22−(√2)2=P(2−√2)4−2=P(2−√2)2
Step 6: Calculate the area of the triangle
The area A of triangle ABC can be calculated using the formula:
A=12×base×height
In this case, both the base and height are equal to a:
A=12×a×a=12a2
Step 7: Substitute a into the area formula
Now substitute the expression for a:
A=12(P(2−√2)2)2
Calculating a2:
a2=(P(2−√2)2)2=P2(2−√2)24
Thus,
A=12⋅P2(2−√2)24=P2(2−√2)28
Step 8: Expand (2−√2)2
Calculating (2−√2)2:
(2−√2)2=4−4√2+2=6−4√2
Thus, the area becomes:
A=P2(6−4√2)8
Final Result
The area of the triangle ABC is:
A=P2(6−4√2)8
An isosceles right triangle has two equal sides and a right angle (90 degrees) between them. Let's denote the lengths of the equal sides as a and the hypotenuse as AC.
The perimeter P of triangle ABC can be expressed as:
P=AB+BC+AC=a+a+AC=2a+AC
According to the Pythagorean theorem:
AC2=AB2+BC2
Since AB=a and BC=a:
AC2=a2+a2=2a2
Thus, we can find AC:
AC=√2a2=a√2
Now substitute AC back into the perimeter equation:
P=2a+a√2
This can be rearranged to find a:
P=a(2+√2)
So,
a=P2+√2
To simplify a, we can rationalize the denominator:
a=P(2−√2)(2+√2)(2−√2)=P(2−√2)22−(√2)2=P(2−√2)4−2=P(2−√2)2
The area A of triangle ABC can be calculated using the formula:
A=12×base×height
In this case, both the base and height are equal to a:
A=12×a×a=12a2
Now substitute the expression for a:
A=12(P(2−√2)2)2
Calculating a2:
a2=(P(2−√2)2)2=P2(2−√2)24
Thus,
A=12⋅P2(2−√2)24=P2(2−√2)28
Calculating (2−√2)2:
(2−√2)2=4−4√2+2=6−4√2
Thus, the area becomes:
A=P2(6−4√2)8
The area of the triangle ABC is:
A=P2(6−4√2)8
Topper's Solved these Questions
Similar Questions
Knowledge Check
In an isosceles right angled triangle the perimeter is 20 meter find its area
A9320m2B8750m2C7980m2D8000m2In an isosceles right - angled triangle , the perimeter is 30 m . Find its area (Approximate) .
A38.63m2B40m2C39.60m2D37.86m2ABC is an isosceles right anlged triangle with AB = BC = 1 . If P is any point on AC, then min (max {(area APQ) , (area PQBR) , area PRC )}} is
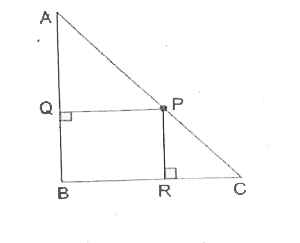 A29B19C13Dnone of these
A29B19C13Dnone of these
The altitude drawn to the base of an isosceles triangle is 8 cm and the perimeter is 32 cm. Find the area of the triangle.
View SolutionIf perimeter of an isoceles right angled Δ is P . Then find the area of this triangle .
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
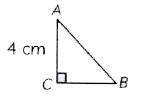
View SolutionIn Figure ABC is an isosceles triangle right angled at C with AC = 4 cm . Find the length of AB .
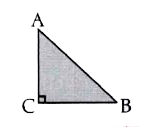
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View Solution