In ΔPQR,∠P is a right angle and PT is perpendicular to QR. If PT=4cmQR=12cm, then the value of (cotQ+cotR) is
The correct Answer is:3
To solve the problem, we need to find the value of cotQ+cotR in triangle ΔPQR where ∠P is a right angle, PT is perpendicular to QR, PT=4cm, and QR=12cm.
1. Understanding the Triangle:
- In triangle PQR, since ∠P is a right angle, we can denote the lengths of the sides as follows:
- Let PQ=a
- Let PR=b
- The hypotenuse QR=c=12cm
2. Using the Definition of Cotangent:
- The cotangent of an angle in a right triangle is defined as the ratio of the adjacent side to the opposite side.
- Therefore, we have:
cotQ=PQPTandcotR=PRPT
3. Finding the Lengths of PQ and PR:
- From triangle PTQ:
- PT=4cm
- Let QT=x (the length of QT).
- Using the Pythagorean theorem in triangle PTQ:
PQ2=PT2+QT2⟹a2=42+x2⟹a2=16+x2(1)
- From triangle PTR:
- Let RT=y (the length of RT).
- Again using the Pythagorean theorem:
PR2=PT2+RT2⟹b2=42+y2⟹b2=16+y2(2)
4. Relating QT and RT:
- Since QT+RT=QR=12cm:
x+y=12(3)
5. Expressing y in terms of x:
- From equation (3), we can express y as:
y=12−x(4)
6. Substituting y into Equation (2):
- Substitute y from equation (4) into equation (2):
b2=16+(12−x)2
- Expanding this:
b2=16+(144−24x+x2)⟹b2=160−24x+x2(5)
7. Finding cotQ+cotR:
- Now, we can find cotQ+cotR:
cotQ+cotR=PQPT+PRPT=PQ+PRPT=a+b4
- From equations (1) and (5), we can find a+b:
- Since a2+b2=c2 (Pythagorean theorem):
a2+b2=122=144
- We can also express a+b in terms of x:
a+b=√16+x2+√160−24x+x2
8. Final Calculation:
- However, we can simplify our calculation:
cotQ+cotR=QRPT=124=3
Final Answer:
Thus, the value of cotQ+cotR is 3.
- In triangle PQR, since ∠P is a right angle, we can denote the lengths of the sides as follows:
- Let PQ=a
- Let PR=b
- The hypotenuse QR=c=12cm
- The cotangent of an angle in a right triangle is defined as the ratio of the adjacent side to the opposite side.
- Therefore, we have:
cotQ=PQPTandcotR=PRPT
- From triangle PTQ:
- PT=4cm
- Let QT=x (the length of QT).
- Using the Pythagorean theorem in triangle PTQ:
PQ2=PT2+QT2⟹a2=42+x2⟹a2=16+x2(1)
- From triangle PTR:
- Let RT=y (the length of RT).
- Again using the Pythagorean theorem:
PR2=PT2+RT2⟹b2=42+y2⟹b2=16+y2(2)
- Since QT+RT=QR=12cm:
x+y=12(3)
- From equation (3), we can express y as:
y=12−x(4)
- Substitute y from equation (4) into equation (2):
b2=16+(12−x)2
- Expanding this:
b2=16+(144−24x+x2)⟹b2=160−24x+x2(5)
- Now, we can find cotQ+cotR:
cotQ+cotR=PQPT+PRPT=PQ+PRPT=a+b4
- From equations (1) and (5), we can find a+b:
- Since a2+b2=c2 (Pythagorean theorem):
a2+b2=122=144
- We can also express a+b in terms of x:
a+b=√16+x2+√160−24x+x2
- However, we can simplify our calculation:
cotQ+cotR=QRPT=124=3
Thus, the value of cotQ+cotR is 3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC,∠A is right angle and AD is perpendicular to BC . If AD=4cm,BC=12 cm, then value of (cotB+cotC) is
A6B3C4D32 - Question 2 - Select One
In ΔPQR,Q is a right angle, PQ = 3 and QR = 4. If ∠P=αandR=β, then tan β is equal to
A43B34C35D53 - Question 3 - Select One
In ΔPQR,Q is a right angle, PQ=3andQR=4. If ∠P=αandR=β, then tanβ is equal to
A43B34C35D53
In ΔPQR , with ∠Q at right angle, given that PR+QR=25 cm and PQ=5 cm . Find the value of :
(i) sinP,cosP and tanP .
(ii) secR−cotP .
 View Solution
View SolutionΔPQR is right angled at point Q. If PQ=8cmand PR=(QR+2)cm. What is the value (in cm) of PR?
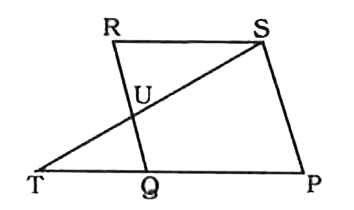
View SolutionIn the given figure, PQRSis a parallelogram and U is the mid point of QR. If PQ=4cm, then what is the value of PT (in cm.)?
 View Solution
View SolutionIn the given figure, PQRSis a parallelogram and U is the mid point of QR. If PQ=4cm, then what is the value of PT (in cm.)?
 View Solution
View SolutionTriangle PQR circumscribes a circle with centre O and radius r cm such that ∠PQR=90∘. If PQ=3cm,QR=4cm, then the value of r is :
View Solution
