In ΔPQR,Q is a right angle, PQ=3andQR=4. If ∠P=αandR=β, then tanβ is equal to
43
34
35
53
The correct Answer is:B
To solve the problem, we need to find the value of tanβ in triangle PQR where Q is the right angle, PQ=3, and QR=4.
1. Identify the Triangle and Angles:
- In triangle PQR, angle Q is the right angle.
- Let ∠P=α and ∠R=β.
2. Identify the Sides:
- The side opposite to angle R (which is β) is PQ.
- The side adjacent to angle R is QR.
- Given values:
- PQ=3 (opposite side to β)
- QR=4 (adjacent side to β)
3. Use the Definition of Tangent:
- The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side.
- Therefore, we can write:
tanβ=OppositeAdjacent=PQQR
4. Substitute the Values:
- Now substitute the known values into the equation:
tanβ=PQQR=34
5. Conclusion:
- Thus, the value of tanβ is:
tanβ=34
Final Answer:
tanβ=34
- In triangle PQR, angle Q is the right angle.
- Let ∠P=α and ∠R=β.
- The side opposite to angle R (which is β) is PQ.
- The side adjacent to angle R is QR.
- Given values:
- PQ=3 (opposite side to β)
- QR=4 (adjacent side to β)
- The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side.
- Therefore, we can write:
tanβ=OppositeAdjacent=PQQR
- Now substitute the known values into the equation:
tanβ=PQQR=34
- Thus, the value of tanβ is:
tanβ=34
tanβ=34
Topper's Solved these Questions
- TRIGNOMETRIC RATIOS Book:ARIHANT PUBLICATION JHARKHANDChapter:TRIGNOMETRIC RATIOS Exercise:Exam Booster for Cracking Exam
Explore 25 Videos
- TIME AND WORKBook:ARIHANT PUBLICATION JHARKHANDChapter:TIME AND WORKExercise:Exam Booster for Cracking Exam
Explore 18 Videos
- TRIGONOMETRIC IDENTITIESBook:ARIHANT PUBLICATION JHARKHANDChapter:TRIGONOMETRIC IDENTITIESExercise:EXAM BOOSTER FOR CRACKING EXAM
Explore 35 Videos
Similar Questions
Knowledge Check
In ΔPQR, If ∠R>∠Q, then
AQR>PRBPQ>PRCPQ<PRDQR>PRIn ΔPQR,PQ=6√3cm,PR=12cmandQR=6cm then ∠Q is
A45∘B60∘C90∘D120∘In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
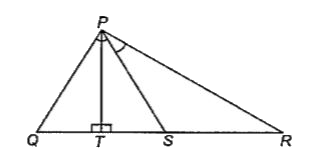 A10B30C60D15
A10B30C60D15
In ΔPQR, if PQ=QR and ∠Q=100°, then ∠R is equal to
View SolutionIn ΔPQR it is given that = PQPR=QSSR. If ∠Q=70∘and∠R=50∘ then ∠QPS = ?
View SolutionIn △PQR, right angled at Q, PQ=105 and QR=208, the value of tanR is:
View SolutionIn △PQR,∠Q≻∠R, PS is the bisector of ∠P and PT⊥QR. If ∠SPT=28∘ and ∠R=23∘ , then the measure of ∠Q is:
त्रिभुज PQR में, ∠Q≻∠R, है तथा PS कोण P का समद्विभाजक है और PT⊥QR है । यदि ∠SPT=28∘ और ∠R=23∘ है, तो कोण Q का मान क्या है?
View SolutionΔPQR is right angled at Q. If ∠R=30∘, then find the value of (cos P -1/3).
View Solution

