In a rectangle ABCD, AB= 15 cm ∠BAC=60∘ then BC is equal to
15√2cm
15cm
15√5cm
15√3cm
The correct Answer is:D
Step by step video, text & image solution for In a rectangle ABCD, AB= 15 cm angle BAC = 60^@ then BC is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGNOMETRIC RATIOS BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - TRIGNOMETRIC RATIOS EXERCISE - Exam Booster for Cracking Exam
25 Videos
- TIME AND WORKBOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - TIME AND WORKEXERCISE - Exam Booster for Cracking Exam
18 Videos
- TRIGONOMETRIC IDENTITIESBOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - EXAM BOOSTER FOR CRACKING EXAM
35 Videos
Similar Questions
In a rectangle ABCD, AB = 25 cm and BC = 15. In what ratio does the bisector of ∠C divide AB?
View SolutionIn a △ABC, AD is perpendicular to BC from A, if ∠BAC=90∘, then AB2:AC2 is equal to :
त्रिभुज ABC में, AD, A से BC पर डाला गया लम्ब है | यदि ∠BAC=90∘ है, तो AB2:AC2 का मान क्या होगा ?
View Solution
Knowledge Check
In a rectangle ABCD , AB = 15 cm and ∠BAC=60∘, then the length of side BC is
A15√2 cmB15 cmC15√5 cmD15√3 cmIn a right angled ΔABC,∠C=90∘andCD is the perpendicular on hypotenuse AB if BC = 15 cm and AC=20cm then CD is equal to :
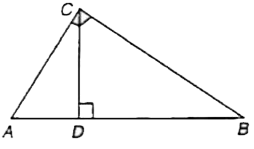 A18 cmB12 cmC17.5 cmDcan't be determined
A18 cmB12 cmC17.5 cmDcan't be determinedIn ΔABC, D is a point on side BC such that ∠ADC=∠BAC, If CA = 12 cm, CB = 8 cm then CD is equal to :
A18 cmB12 cmC16 cmD15 cm
ABCD is a rombus in which angle C = 60∘. Then, BC : AD is equal to
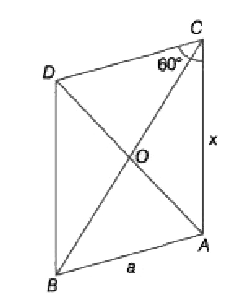
View SolutionIn a rectangle ABCD, AB=20cm , ∠BAC=60o . Calculate side BC .
View Solution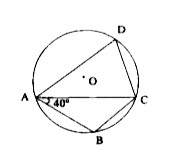
In the figure given above, O is the centre of a circle circumscribing a quadrilateral ABCD. If AB=BC and ∠BAC=40∘, then what is ∠ADC equal to ?
View SolutionIn ΔABC, right-angled at B, AB = 3 cm and ∠BAC =60∘ . Determine the lengths of the sides BC and AC.
View SolutionA paper is in the form of a rectangle ABCD where AB = 21 cm and BC = 14 cm. A semicircular portion with BC as diameter is cut off. Find the area of the remaining paper
View Solution
