In a ΔABC right angle at C .P is the length of ⊥ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
1P2=1a2−1b2
1P2=1b2−1a2
1P2=1a2+1b2
1P2+1a2=1b2=0
The correct Answer is:(iii)
To solve the problem step by step, we will analyze the right triangle ABC, where angle C is the right angle. We will derive the relationship between the sides of the triangle and the height from point C to side AB.
Step 1: Understand the Triangle
We have a right triangle ABC with:
- Angle C = 90 degrees
- Sides:
- BC = a
- CA = b
- AB = c
Step 2: Area of Triangle
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
We can consider different bases and corresponding heights.
Step 3: Using Base AB
If we take AB as the base, the height from C to AB is P. Thus, the area can be expressed as:
Area=12×c×P
Step 4: Using Base BC
Now, if we take BC as the base, the height from A to BC is the same height P. Thus, the area can also be expressed as:
Area=12×a×P
Step 5: Equating the Areas
Since both expressions represent the area of the same triangle, we can equate them:
12×c×P=12×a×P
This simplifies to:
c×P=a×P
Assuming P is not zero, we can divide both sides by P:
c=a
This is not correct since we know that c is the hypotenuse.
Step 6: Using Pythagorean Theorem
Using the Pythagorean theorem, we know:
a2+b2=c2
Step 7: Expressing Area in Terms of Sides
We can also express the area in terms of the sides:
Area=12×a×b
Step 8: Relating Area with Height
We can also express the area using the height:
Area=12×c×P
Equating the two area expressions gives:
12×a×b=12×c×P
Cancelling 12 from both sides, we get:
a×b=c×P
Step 9: Deriving the Final Relation
Rearranging gives us:
P=a×bc
Now, we can use this to derive the relationship:
Using the area again, we can express:
1P=1a+1b
This leads us to:
1c2=1a2+1b2
Final Relation
Thus, the correct relationship is:
1c2=1a2+1b2
We have a right triangle ABC with:
- Angle C = 90 degrees
- Sides:
- BC = a
- CA = b
- AB = c
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
We can consider different bases and corresponding heights.
If we take AB as the base, the height from C to AB is P. Thus, the area can be expressed as:
Area=12×c×P
Now, if we take BC as the base, the height from A to BC is the same height P. Thus, the area can also be expressed as:
Area=12×a×P
Since both expressions represent the area of the same triangle, we can equate them:
12×c×P=12×a×P
This simplifies to:
c×P=a×P
Assuming P is not zero, we can divide both sides by P:
c=a
This is not correct since we know that c is the hypotenuse.
Using the Pythagorean theorem, we know:
a2+b2=c2
We can also express the area in terms of the sides:
Area=12×a×b
We can also express the area using the height:
Area=12×c×P
Equating the two area expressions gives:
12×a×b=12×c×P
Cancelling 12 from both sides, we get:
a×b=c×P
Rearranging gives us:
P=a×bc
Now, we can use this to derive the relationship:
Using the area again, we can express:
1P=1a+1b
This leads us to:
1c2=1a2+1b2
Thus, the correct relationship is:
1c2=1a2+1b2
Topper's Solved these Questions
Similar Questions
ABC is a triangle right-angled at C. If p is the length of the perpendicular from C to AB and a, b, c are the sides, then which one of the following is correct ?
View SolutionIn ΔABC, C is right angle and a perpendicular 'p' is drawn on side AB. If a, b, c are length of sides BC, CA, AB respectively then which of the following is correct?
View Solution
Knowledge Check
In a ΔABC right angle at C .P is the length of ⊥ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A1p2=1b2−1a2B1p2=1a2+1b2C1p2+1a2=−1b2D1p2=1a2−1b2ΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
A17B7C13D14In a right triangle ABC, in which ∠C=90∘amdCD⊥AB. If BC =a, CA=b, AB=c and CD=p, then
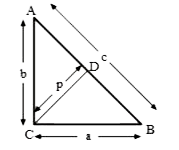 A1p2=1a2+1b2B1p2≠1a2+1b2C1p2<1a2+1b2D1p2>1a2+1b2
A1p2=1a2+1b2B1p2≠1a2+1b2C1p2<1a2+1b2D1p2>1a2+1b2
ABC is a triangle right angled at C with BC = a and AC = b. If p is the length of the perpendicular from C on AB, then which one of the following is correct ?
View SolutionIn ΔABC, right-angled at B, AB = 3 cm and ∠BAC =60∘ . Determine the lengths of the sides BC and AC.
View SolutionABC is a right traingle, right angled at C. if P is the length of perpendicular from C to AB and AB=c, BC=a and CA=b, then prove that (i) pc=ab (ii) 1p2=1a2+1b2
View SolutionABC is a triangle right angled at C. Let p be the length of the perpendicular drawn from C on AB. If BC = 6 cm and CA = 8 cm, then what is the value of p ?
View SolutionIn △ABC right angled at B, if the two sides AB and BC are in the ratio 1 : 3, evaluate the value of sin C.
View Solution
