ΔABC is right angled at A, AB=3 units ,AC=4 units and AD is perpendicular to BC. What is the area of the ΔADB
The correct Answer is:5425
To find the area of triangle ADB, we will follow these steps:
Step 1: Find the length of side BC using the Pythagorean theorem.
Given that triangle ABC is right-angled at A, with sides AB = 3 units and AC = 4 units, we can use the Pythagorean theorem:
BC2=AB2+AC2
Calculating the squares:
BC2=32+42=9+16=25
Taking the square root:
BC=√25=5 units
Step 2: Calculate the area of triangle ABC.
The area of triangle ABC can be calculated using the formula:
Area=12×base×height
Here, we can take AB as the base and AC as the height:
AreaABC=12×AB×AC=12×3×4=6 square units
Step 3: Relate the areas of triangles ABC and ADB.
Since AD is perpendicular to BC, we can express the area of triangle ABC in terms of triangle ADB:
AreaABC=AreaADB+AreaADC
Step 4: Use the formula for the area of triangle ABC to find AD.
We know that:
AreaABC=12×BC×AD
Substituting the known values:
6=12×5×AD
Multiplying both sides by 2:
12=5×AD
Solving for AD:
AD=125 units
Step 5: Find the length of BD using the relation in triangle ADB.
Using the relation from triangle ABC:
AB2=BD×BC
Substituting the known values:
32=BD×5
Calculating:
9=5×BD
Solving for BD:
BD=95 units
Step 6: Calculate the area of triangle ADB.
Now we can find the area of triangle ADB using the base BD and height AD:
AreaADB=12×BD×AD
Substituting the values:
AreaADB=12×95×125
Calculating:
=12×10825=5425 square units
Final Answer:
The area of triangle ADB is 5425 square units.
---
Given that triangle ABC is right-angled at A, with sides AB = 3 units and AC = 4 units, we can use the Pythagorean theorem:
The area of triangle ABC can be calculated using the formula:
Since AD is perpendicular to BC, we can express the area of triangle ABC in terms of triangle ADB:
We know that:
Using the relation from triangle ABC:
Now we can find the area of triangle ADB using the base BD and height AD:
The area of triangle ADB is 5425 square units.
Topper's Solved these Questions
Similar Questions
Knowledge Check
ΔABC is right angled at A and AB = 10 units .AC = 30 units and AD is perpendicular to BC. What is the area of ΔADB ?
A20B18C15D150If ΔABC is right - angle at B, AB = 6 units ∠=30∘ then AC is equal to
A12 unitsB15 unitsC8 unitsD10 unitsIn triangle ABC, AD is prependicular to BC and DE is perpendicular to AB
 AabcdprqqBabcdqrpsCabcdspqrDabcdrpsq
AabcdprqqBabcdqrpsCabcdspqrDabcdrpsq
ΔABC is right angled at A (Fig 11.25). AD is perpendicular to BC. If AB=5cm,BC=13 and, find the area of ΔABC Also find the lenght of AD.
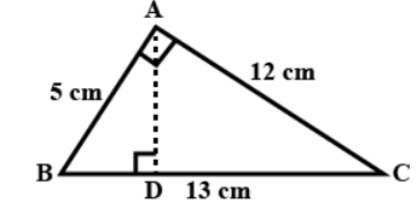
View SolutionΔABC is right-angled at A and AD⊥BC. If BC=13cmandAC=5cm, find the ratio of areas of ΔABCandΔADC.

View SolutionIn the following figure, (not to scale) ABC is triangle, where AB=1 unit, BC=√3 units and AC=2 units
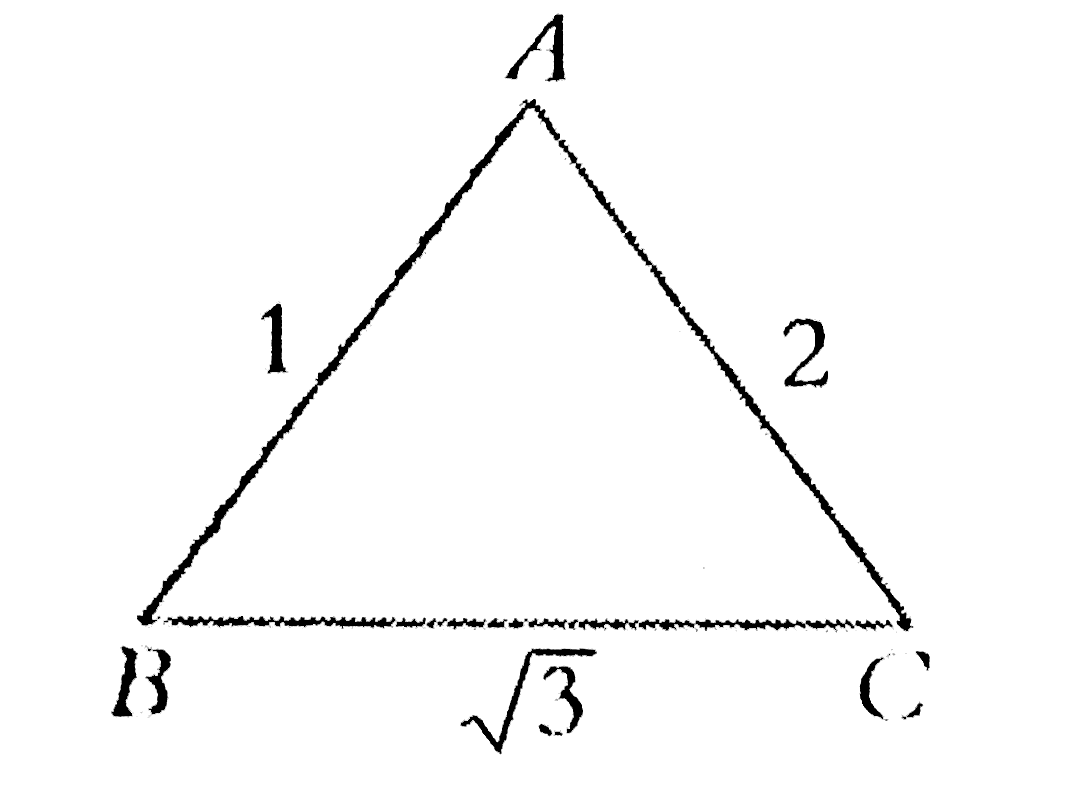
What is the relationship among AB,BC and CA?
View SolutionΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC=16cmBC=9cm, find the length of CD.
View Solution. In right angled triangle ABC,∠A is right angle. AD is perpendicular to the hypotenuse BC. Prove that ΔABCΔACD=BC2AC2
View Solution
