In ΔABC,∠A is right angle and AD is perpendicular to BC . If AD=4cm,BC=12 cm, then value of (cotB+cotC) is
6
3
4
32
The correct Answer is:B
To solve the problem, we need to find the value of cotB+cotC in triangle ΔABC where ∠A is a right angle, AD is perpendicular to BC, AD=4cm, and BC=12cm.
1. Identify the Given Values:
- AD=4cm
- BC=12cm
2. Use the Area of Triangle:
The area of triangle ABC can be calculated using the base BC and height AD:
Area=12×BC×AD=12×12×4=24cm2
3. Relate the Area to Sides AB and AC:
The area can also be expressed in terms of sides AB and AC as:
Area=12×AB×AC
Therefore, we have:
AB×AC=48
4. Express AB and AC in Terms of Angles:
Using the definitions of sine:
AB=ADsinB=4sinB
AC=ADsinC=4sinC
Now substitute these into the area equation:
(4sinB)(4sinC)=48
Simplifying gives:
16sinBsinC=48
Thus:
sinBsinC=1648=13
5. Find cotB+cotC:
We know:
cotB=cosBsinB,cotC=cosCsinC
Therefore:
cotB+cotC=cosBsinB+cosCsinC=cosBsinC+cosCsinBsinBsinC
Using the identity sin(B+C)=sin(90∘)=1:
sinBcosC+cosBsinC=sin(B+C)=1
Thus:
cotB+cotC=1sinBsinC
6. Substitute the Value of sinBsinC:
cotB+cotC=113=3
Final Answer:
The value of cotB+cotC is 3.
- AD=4cm
- BC=12cm
The area of triangle ABC can be calculated using the base BC and height AD:
Area=12×BC×AD=12×12×4=24cm2
The area can also be expressed in terms of sides AB and AC as:
Area=12×AB×AC
Therefore, we have:
AB×AC=48
Using the definitions of sine:
AB=ADsinB=4sinB
AC=ADsinC=4sinC
Now substitute these into the area equation:
(4sinB)(4sinC)=48
Simplifying gives:
16sinBsinC=48
Thus:
sinBsinC=1648=13
We know:
cotB=cosBsinB,cotC=cosCsinC
Therefore:
cotB+cotC=cosBsinB+cosCsinC=cosBsinC+cosCsinBsinBsinC
Using the identity sin(B+C)=sin(90∘)=1:
sinBcosC+cosBsinC=sin(B+C)=1
Thus:
cotB+cotC=1sinBsinC
cotB+cotC=113=3
The value of cotB+cotC is 3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
∠Aof ΔABC is a right angle. AD is perpendicular on BC. If BC = 14 cm and BD = 5 cm, then measure of AD is :
A2√5cm.B√5cm.C3√5cm.D3.5√5cm.In triangle ABC,∠BAC=90∘and AD is perpendicular to BC. If AD=6cmand BD=4cm, then the length of BC is:
A10 cmB12 cmC13 cmD15 cm.In ΔABC,∠BAC=90∘andAD is drawn perpendicular to BC . If BD -=7 cm and CD = 28 cm , what is the length (in cm ) of Ad ?
A3.5B7C10.5D14
Prove that ΔABC is isosceles if median AD is perpendicular to BC.
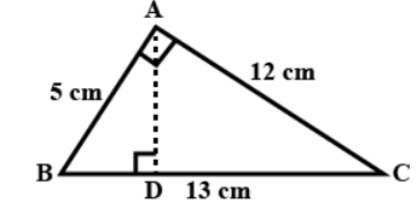
View SolutionΔABC is right angled at A (Fig 11.25). AD is perpendicular to BC. If AB=5cm,BC=13 and, find the area of ΔABC Also find the lenght of AD.
View SolutionABC is a triangle right angled at A and AD is perpendicular to BC. If BD = 8 cm and DC =12.5 cm, then what is AD equal to ?
View SolutionΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC = 16 cm, BC = 12 cm, find the length of CD.
View SolutionIn ΔABC,∠BAC=90∘andAD is drawn perpendicular to BC . If BD -=7 cm and CD = 28 cm , what is the length (in cm ) of Ad ?
View Solution
