In ΔABC there are 2 points D and E on BC such that BD:DE:EC=3:4:5, if the area of ΔADE=40cm2 then find the area of ΔABC .
The correct Answer is:120
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Understanding the Ratios:
We are given that the segments on line BC are in the ratio BD:DE:EC=3:4:5. Let's denote:
- BD=3x
- DE=4x
- EC=5x
2. Finding the Total Length of BC:
The total length of BC can be calculated as:
BC=BD+DE+EC=3x+4x+5x=12x
3. Area of Triangle ADE:
We know that the area of triangle ADE is given as 40cm2.
4. Calculating the Area of Triangle ADE:
The area of triangle ADE can be expressed as:
AreaADE=12×DE×h
where h is the height from point A to line BC. Since DE=4x, we have:
AreaADE=12×4x×h=2xh
Setting this equal to the given area:
2xh=40⟹xh=20(Equation 1)
5. Calculating the Area of Triangle ABC:
The area of triangle ABC can be expressed as:
AreaABC=12×BC×h=12×12x×h=6xh
Substituting xh from Equation 1:
AreaABC=6×20=120cm2
6. Final Answer:
Therefore, the area of triangle ABC is:
AreaABC=120cm2
We are given that the segments on line BC are in the ratio BD:DE:EC=3:4:5. Let's denote:
- BD=3x
- DE=4x
- EC=5x
The total length of BC can be calculated as:
BC=BD+DE+EC=3x+4x+5x=12x
We know that the area of triangle ADE is given as 40cm2.
The area of triangle ADE can be expressed as:
AreaADE=12×DE×h
where h is the height from point A to line BC. Since DE=4x, we have:
AreaADE=12×4x×h=2xh
Setting this equal to the given area:
2xh=40⟹xh=20(Equation 1)
The area of triangle ABC can be expressed as:
AreaABC=12×BC×h=12×12x×h=6xh
Substituting xh from Equation 1:
AreaABC=6×20=120cm2
Therefore, the area of triangle ABC is:
AreaABC=120cm2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔABC, a line through a cuts the side BC at D such that BD : CD = 4: 5. If the area of ΔABD=60cm2, then the area of ΔADC is
A90cm2B50cm2C60cm2D75cm2In ΔABC , a line through A cuts the side BC at D such that BD :DC =4 :5 if the area of ΔABD=60cm2 , then the area of ΔADC is
A90cm2B50cm2C60cm2D75cm2Two persons K and L enter into a business by investing their sum in the ratio of 7 : 9. After 7 months, L leaves the business. After eleven month, if total profit is Rs. 2460, what is the profit share of L (in Rs)?
AA) Rs, 1109BB) Rs. 1107CC) Rs. 1111DD) Rs. 1113
In the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View SolutionIf ΔABC~ΔDEF,BC=3cm,EF=4cm and area of ΔABC=54sqcm then find the area of ΔDEF
View SolutionIn a Δ ABC , DE||BC if DE=23 BC and area of ΔABC =81cm2 find the area of ΔADE
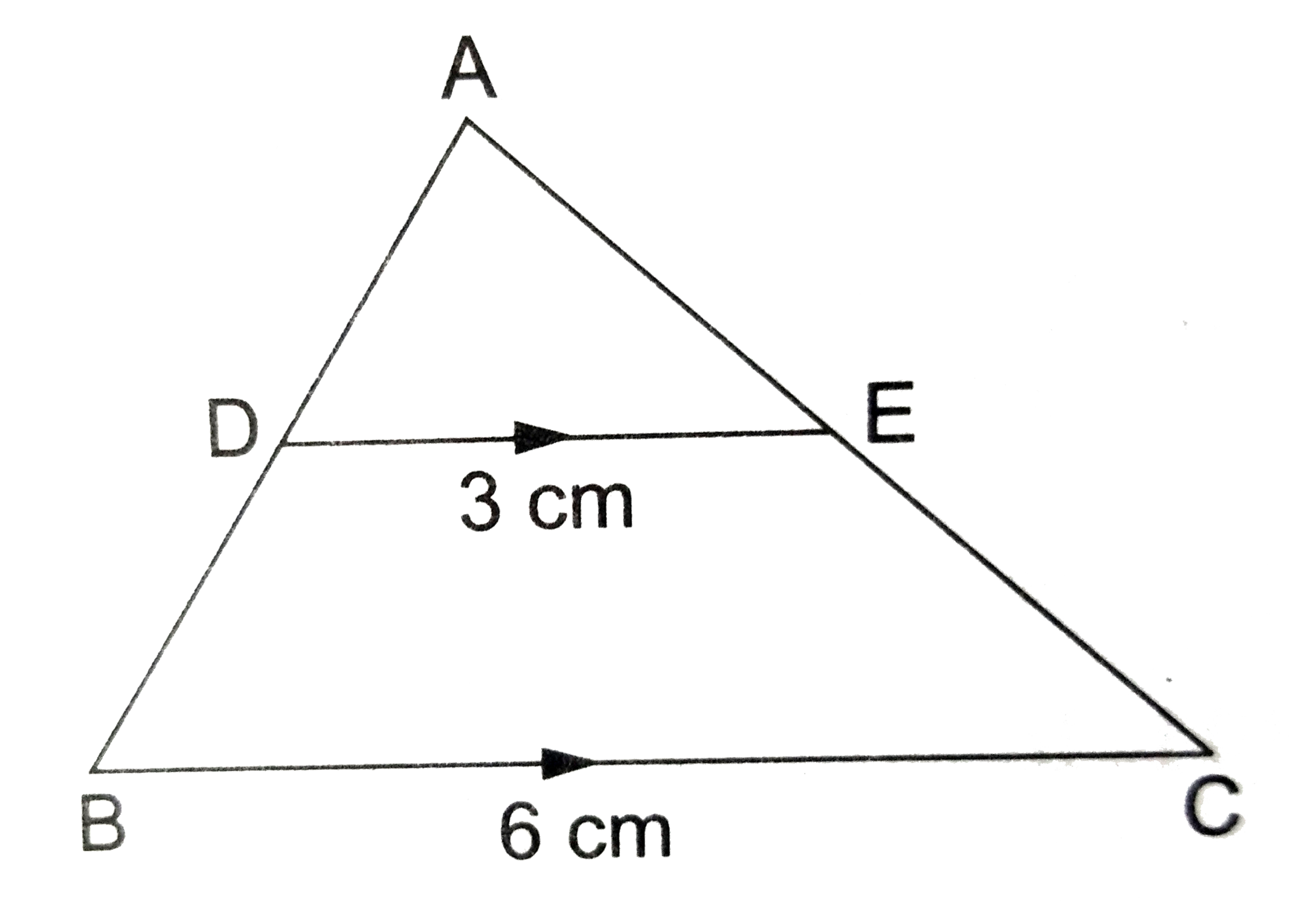
View SolutionIn the given figure, DE∣∣BC. If DE=3cm,BC=6andar(ΔADE)=15cm2, find the area of ΔABC.
View SolutionIf ΔABC is similar to ΔDEF such that BC = 3 cm, EF = 4 cm and area of ΔABC=54cm2, then the area of ΔDEF is :
View Solution