Question

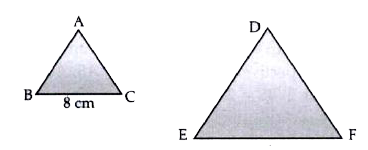
If $\Delta ABC$ is similar to $\Delta DEF$ such that BC = 3 cm, EF = 4 cm and area of $\Delta ABC=54c{m}^2$, then the area of $\Delta DEF$ is :

Options

A. `66 cm^(2)`
B. `78 cm^(2)`
C. `96 cm^(2)`
D. `54 cm^(2)`

Answer

C

Explanation

To find the area of triangle DEF given that triangle ABC is similar to triangle DEF, we can use the properties of similar triangles. Here’s how to solve the problem step by step:

1. Identify the given values:
- Side BC of triangle ABC = 3 cm
- Side EF of triangle DEF = 4 cm
- Area of triangle ABC = 54 cm²

2. Set up the ratio of the sides:
Since triangles ABC and DEF are similar, the ratio of their corresponding sides is equal to the ratio of their areas. The ratio of the sides is:
\( \text{Ratio of sides} = \frac{BC}{EF} = \frac{3}{4} \)

3. Calculate the ratio of the areas:
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore:
\( \text{Ratio of areas} = \left(\frac{BC}{EF}\right)^2 = \left(\frac{3}{4}\right)^2 = \frac{9}{16} \)

4. Set up the equation for the areas:
Let the area of triangle DEF be \( A_{DEF} \). We can set up the following proportion based on the areas:
\( \frac{Area_{ABC}}{Area_{DEF}} = \frac{9}{16} \)
Substituting the known area of triangle ABC:
\( \frac{54}{A_{DEF}} = \frac{9}{16} \)

5. Cross-multiply to solve for \( A_{DEF} \):
\( 54 \times 16 = 9 \times A_{DEF} \)
\( 864 = 9 \times A_{DEF} \)

6. Divide both sides by 9:
\( A_{DEF} = \frac{864}{9} = 96 \text{ cm}^2 \)

Final Answer:
The area of triangle DEF is 96 cm².