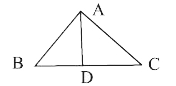
In a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
20cm2
30cm2
40cm2
25cm2
The correct Answer is:B
Step by step video & text solution for In a Delta ABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of Delta ABC=72 cm^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - III
Explore 21 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - IV
Explore 169 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:Test Yourself
Explore 28 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
Knowledge Check
In a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
A12 cm2B16cm2C24cm2D8cm2If O is the centroid and AD, BE and CF are the three medians of ΔABC with an area of 96cm2 then the area of ΔBOD in cm2 is
A8B12C16D24In a ΔABC,AD,BE and CF are three medians. The perimeter of ΔABC is always.
Aequal to (¯¯¯¯¯¯AB+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF)Bgreater than (¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF)Cless than (¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF)DNone of these
In the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View Solution
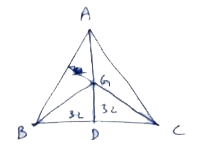
In the above ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE,and¯¯¯¯¯¯CF are the medians. G is the centroid. What is the ratio of the areas of ΔBGDandΔGCE?
View SolutionIn a ΔABC,AD is median, G is a Mid point of AD. If area of ΔAGC IS 32 SQ . units then find area of ΔBGC
View SolutionIn A ΔABC,AD,BEandCF are three medians . The perimeter of ΔABC is always
View SolutionIn an equilateral ΔABC, the medians AD, BE and CF interest to each other at point G. If the area of quadrilateral BDGF is 12√3cm3, then the side of ΔABC is:
View Solution