Two rods A and B of same area of cross-section are joined together end to end The free end of the rod A is kept in melting ice at 300 K and free end of B rod at 400 K. The rods are of the same length. The conductivity of A is 3 times that of B. Calculate the temperature of the junction of the rods.
The correct Answer is:325 K
To solve the problem, we will follow these steps:
Step 1: Understand the setup
We have two rods A and B joined end to end. Rod A is at 300 K (melting ice) and rod B is at 400 K. The thermal conductivity of rod A is three times that of rod B.
Step 2: Define the variables
Let:
- k2 = thermal conductivity of rod B
- k1=3k2 = thermal conductivity of rod A
- L = length of both rods (same for both)
- A = cross-sectional area (same for both)
- θ = temperature at the junction of the rods
Step 3: Write the heat flow equations
According to Fourier's law of heat conduction, the rate of heat flow Q/t through a rod is given by:
Qt=k⋅A⋅(T1−T2)L
For rod A, the heat flow is:
Qt=k1⋅A⋅(θ−300)L
For rod B, the heat flow is:
Qt=k2⋅A⋅(400−θ)L
Step 4: Set the heat flows equal
Since the heat flow through both rods is the same, we can set the two equations equal to each other:
k1⋅A⋅(θ−300)L=k2⋅A⋅(400−θ)L
We can cancel A and L from both sides:
k1(θ−300)=k2(400−θ)
Step 5: Substitute k1 in terms of k2
Substituting k1=3k2:
3k2(θ−300)=k2(400−θ)
Now, divide both sides by k2 (assuming k2≠0):
3(θ−300)=400−θ
Step 6: Simplify the equation
Expanding the left side:
3θ−900=400−θ
Now, add θ to both sides:
3θ+θ−900=400
This simplifies to:
4θ−900=400
Step 7: Solve for θ
Add 900 to both sides:
4θ=1300
Now, divide by 4:
θ=13004=325 K
Final Answer
The temperature of the junction of the rods is 325 K.
---
We have two rods A and B joined end to end. Rod A is at 300 K (melting ice) and rod B is at 400 K. The thermal conductivity of rod A is three times that of rod B.
Let:
- k2 = thermal conductivity of rod B
- k1=3k2 = thermal conductivity of rod A
- L = length of both rods (same for both)
- A = cross-sectional area (same for both)
- θ = temperature at the junction of the rods
According to Fourier's law of heat conduction, the rate of heat flow Q/t through a rod is given by:
Qt=k⋅A⋅(T1−T2)L
For rod A, the heat flow is:
Qt=k1⋅A⋅(θ−300)L
For rod B, the heat flow is:
Qt=k2⋅A⋅(400−θ)L
Since the heat flow through both rods is the same, we can set the two equations equal to each other:
k1⋅A⋅(θ−300)L=k2⋅A⋅(400−θ)L
We can cancel A and L from both sides:
k1(θ−300)=k2(400−θ)
Substituting k1=3k2:
3k2(θ−300)=k2(400−θ)
Now, divide both sides by k2 (assuming k2≠0):
3(θ−300)=400−θ
Expanding the left side:
3θ−900=400−θ
Now, add θ to both sides:
3θ+θ−900=400
This simplifies to:
4θ−900=400
Add 900 to both sides:
4θ=1300
Now, divide by 4:
θ=13004=325 K
The temperature of the junction of the rods is 325 K.
Topper's Solved these Questions
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THE RATE OF INCREASE OF THICKNESS OF ICE ON A LAKE
3 Videos
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THERMAL RESISTANCE
7 Videos
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM RATE OF HEAT FLOW
6 Videos
- SELF ASSESSMENT PAPER 5BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-D
6 Videos
- THERMAL RADIATION BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
14 Videos
Similar Questions
Two identical metal rods A and B are joined end to end. The free end of A is kept at 27°C and the free end of B at 37°C. Calculate the temperature of the interface. Thermal conductivity of A=385Wm−1K−1, that of B 110Wm−1K−1.
View SolutionOne end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.
View Solution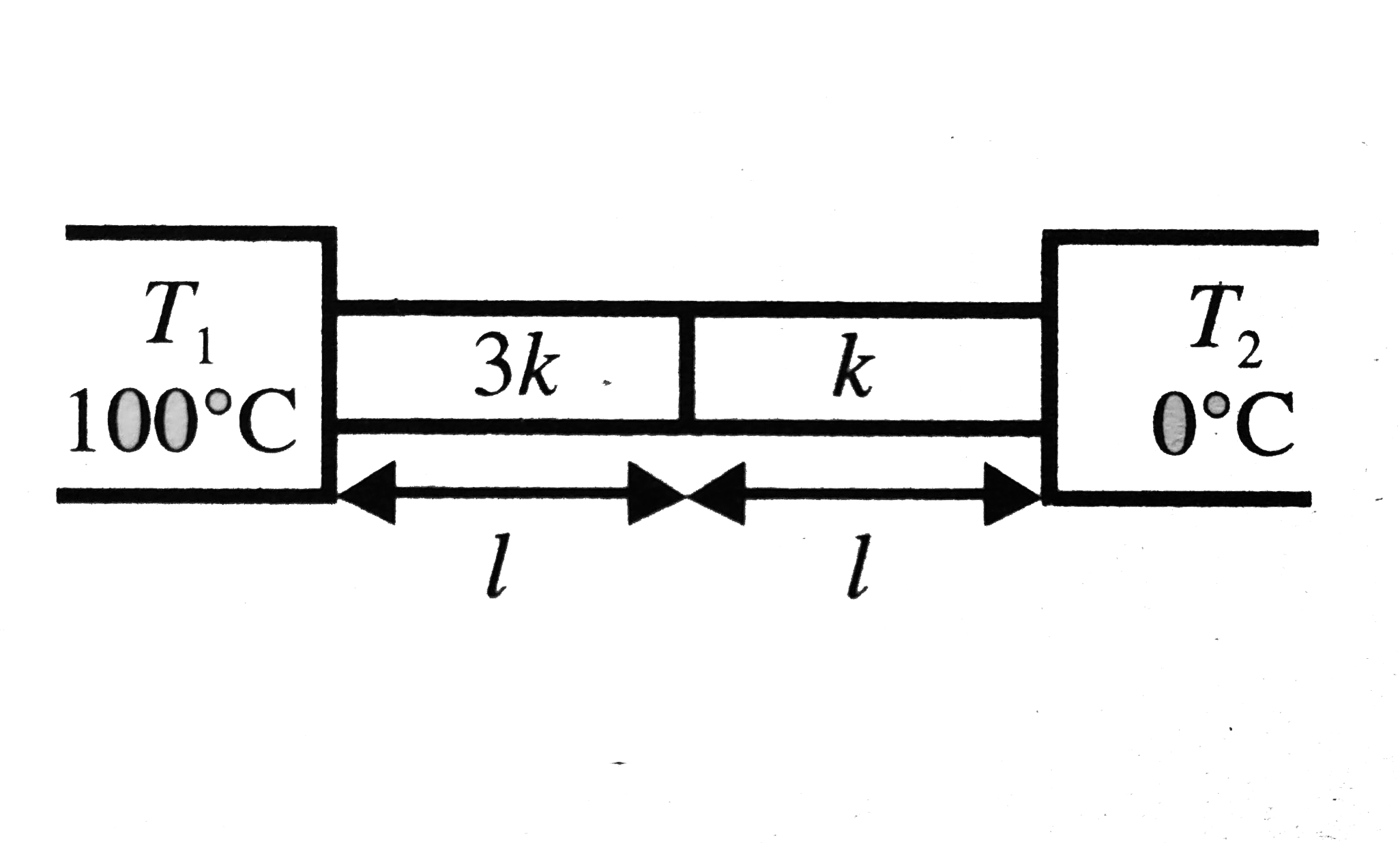
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionTwo rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at 100∘C and 0∘C respectively. The temperature of the junction is 70∘C. Then the temperature of the junction if the rods are inerchanged will be equal to T∘C Find T:
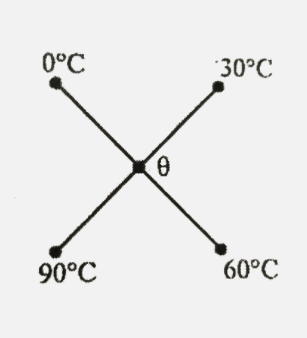
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
View SolutionA copper rod of length 75 cm and an iron rod of length 125cm are joined together end to end . Both are of circular cross section with diameter 2 cm . The free ends of the copper and iron are maintained at 100∘C and0∘C respectively . The surface of the bars are insulated thermally . The temperature of the copper -iron junction is [Thermal conductivity of the copper is 386.4W/m−K and that of iron is 48.46W/m−K].
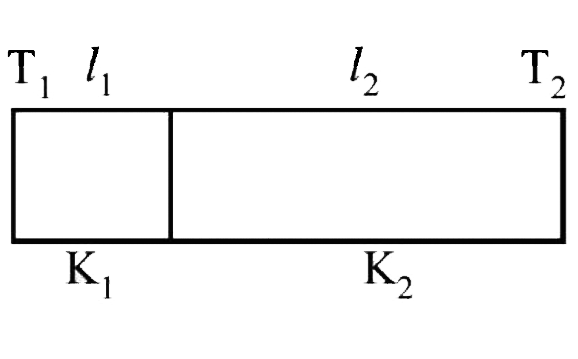
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View Solution