The ratio of the thermal conductivities of two different materials is . The thermal resistance of the rods of these materials having the same thickness are equal. Find the ratio of the length of rods.
The correct Answer is:
To solve the problem step by step, we will use the relationship between thermal resistance, thermal conductivity, and the dimensions of the rods.
Step 1: Understand the Given Information
We are given:
- The ratio of thermal conductivities k1:k2=1:2.
- The thermal resistances of the two rods are equal.
- The thickness of both rods is the same.
Step 2: Define Thermal Resistance
The thermal resistance Rth for a rod can be expressed as:
Rth=Lk⋅A
where:
- L is the length of the rod,
- k is the thermal conductivity,
- A is the cross-sectional area.
Step 3: Write the Thermal Resistance for Both Rods
Let:
- L1 be the length of rod 1,
- L2 be the length of rod 2,
- k1 be the thermal conductivity of rod 1,
- k2 be the thermal conductivity of rod 2.
From the given ratio, we can express:
- k1=k
- k2=2k
Now, we can write the thermal resistances for both rods:
R1=L1k1⋅A=L1k⋅A
R2=L2k2⋅A=L22k⋅A
Step 4: Set the Thermal Resistances Equal
Since the thermal resistances are equal, we can set R1=R2:
L1k⋅A=L22k⋅A
Step 5: Simplify the Equation
We can cancel A and k from both sides (since they are non-zero):
L1=L22
Step 6: Find the Ratio of Lengths
Rearranging the equation gives us:
L1L2=12
Thus, the ratio of the lengths of the rods is:
L1:L2=1:2
Final Answer
The ratio of the lengths of the rods is 1:2.
---
We are given:
- The ratio of thermal conductivities k1:k2=1:2.
- The thermal resistances of the two rods are equal.
- The thickness of both rods is the same.
The thermal resistance Rth for a rod can be expressed as:
Rth=Lk⋅A
where:
- L is the length of the rod,
- k is the thermal conductivity,
- A is the cross-sectional area.
Let:
- L1 be the length of rod 1,
- L2 be the length of rod 2,
- k1 be the thermal conductivity of rod 1,
- k2 be the thermal conductivity of rod 2.
- k1=k
- k2=2k
R1=L1k1⋅A=L1k⋅A
R2=L2k2⋅A=L22k⋅A
Since the thermal resistances are equal, we can set R1=R2:
L1k⋅A=L22k⋅A
We can cancel A and k from both sides (since they are non-zero):
L1=L22
Rearranging the equation gives us:
L1L2=12
L1:L2=1:2
The ratio of the lengths of the rods is 1:2.
Topper's Solved these Questions
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM EXPERIMENT TO DETERMINE K
Explore 2 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM THE RATE OF INCREASE OF THICKNESS OF ICE ON A LAKE
Explore 3 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-D
Explore 6 Videos
- THERMAL RADIATION Book:ICSEChapter:THERMAL RADIATION Exercise:SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)
Explore 14 Videos
Similar Questions
The ratio of thermal conductivites of two different metals is 5:3. In order to have the same thermal resistance in these metals of equal thickness what should be the ratio of their length?
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionThe ratio of the areas of cross section of two rods of different materials is 1:2 and the ratio of ther themal conductivities of their mateirals is 4: 3. On keeping equal temperature difference between the ends of theserods, the rate of conduction of heat are equal. The ratio of the lengths of the rods is
View SolutionThe ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
View Solution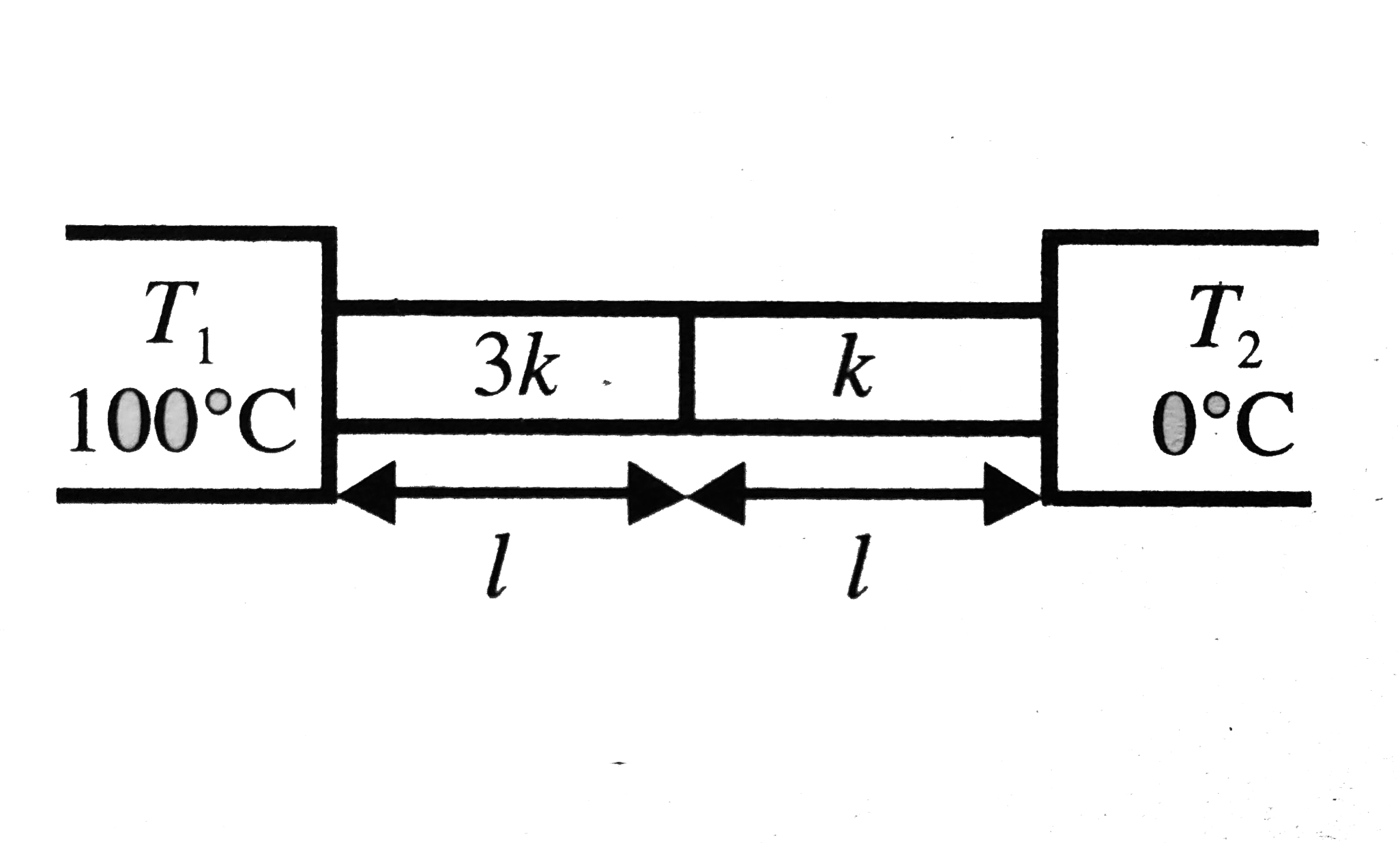
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionTwo spheres made of same substance have diameters in the ratio 1:2. their thermal capacities are in the ratio of
View SolutionThe ratio of radii of two wires of same material is 2:1. If these wires are stretched by equal forces, then the ratio of stresses produced in them will be
View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View SolutionHeat is flowing through two cylindrical rods of the same material . The diameters of the rods are in the ratio 1:2 and the lengths in the ratio 2:1.If the temperature difference between the ends be the same ,then the ratio of the rate of flow if heat through them will be ?
View Solution