Heat is flowing through two cylindrical rods of the same material . The diameters of the rods are in the ratio 1:2 and the lengths in the ratio 2:1.If the temperature difference between the ends be the same ,then the ratio of the rate of flow if heat through them will be ?
To solve the problem, we need to find the ratio of the rate of heat flow through two cylindrical rods with given dimensions. Let's break it down step by step.
Step 1: Understand the given data
- The diameters of the rods are in the ratio d1:d2=1:2.
- The lengths of the rods are in the ratio l1:l2=2:1.
Step 2: Relate diameter to radius
Since the radius is half of the diameter, the ratio of the radii will also be the same:
r1:r2=d12:d22=1:2
Thus, we have:
r1:r2=1:2
Step 3: Write the formula for the rate of heat flow
The rate of heat flow dqdt through a cylindrical rod is given by:
dqdt=k⋅A⋅ΔTL
where:
- k is the thermal conductivity (constant for the same material),
- A is the cross-sectional area,
- ΔT is the temperature difference (same for both rods),
- L is the length of the rod.
Step 4: Calculate the cross-sectional area
The cross-sectional area A of a cylinder is given by:
A=πr2
Thus, for the two rods, we have:
A1=πr21andA2=πr22
Step 5: Substitute the areas into the heat flow formula
Now, we can write the ratio of the rates of heat flow for the two rods:
dq1dtdq2dt=k⋅A1⋅ΔT/L1k⋅A2⋅ΔT/L2
Since k and ΔT are constants, they cancel out:
dq1dtdq2dt=A1⋅L2A2⋅L1
Step 6: Substitute the areas and lengths
Substituting A1=πr21 and A2=πr22:
dq1dtdq2dt=πr21⋅L2πr22⋅L1
The π cancels out:
dq1dtdq2dt=r21⋅L2r22⋅L1
Step 7: Substitute the ratios
Using r1:r2=1:2 and L1:L2=2:1:
- r1=1 and r2=2
- L1=2 and L2=1
Substituting these values:
dq1dtdq2dt=(1)2⋅1(2)2⋅2=1⋅14⋅2=18
Final Answer
Thus, the ratio of the rate of flow of heat through the two rods is:
dq1dt:dq2dt=1:8
- The diameters of the rods are in the ratio d1:d2=1:2.
- The lengths of the rods are in the ratio l1:l2=2:1.
Since the radius is half of the diameter, the ratio of the radii will also be the same:
r1:r2=d12:d22=1:2
Thus, we have:
r1:r2=1:2
The rate of heat flow dqdt through a cylindrical rod is given by:
dqdt=k⋅A⋅ΔTL
where:
- k is the thermal conductivity (constant for the same material),
- A is the cross-sectional area,
- ΔT is the temperature difference (same for both rods),
- L is the length of the rod.
The cross-sectional area A of a cylinder is given by:
A=πr2
Thus, for the two rods, we have:
A1=πr21andA2=πr22
Now, we can write the ratio of the rates of heat flow for the two rods:
dq1dtdq2dt=k⋅A1⋅ΔT/L1k⋅A2⋅ΔT/L2
Since k and ΔT are constants, they cancel out:
dq1dtdq2dt=A1⋅L2A2⋅L1
Substituting A1=πr21 and A2=πr22:
dq1dtdq2dt=πr21⋅L2πr22⋅L1
The π cancels out:
dq1dtdq2dt=r21⋅L2r22⋅L1
Using r1:r2=1:2 and L1:L2=2:1:
- r1=1 and r2=2
- L1=2 and L2=1
dq1dtdq2dt=(1)2⋅1(2)2⋅2=1⋅14⋅2=18
Thus, the ratio of the rate of flow of heat through the two rods is:
dq1dt:dq2dt=1:8
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[Set- II]
Explore 4 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[Set-III]
Explore 3 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-III, DELHI BOARD
Explore 4 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
The ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
View SolutionTwo cylindrical conductors A and B of same metallic material have their diameters in the ratio 1:2 and lengths in the ratio 2:1. If the temperature difference between their ends is same, the ratio of heats conducted respectively by A and B per second is,
View Solution
Knowledge Check
Heat is flowing through two cylindrical rods of the same material. The diamters of the rods are in the ratio 1:2 and the length in the ratio 2:1. If the temperature difference between the ends is same then ratio of the rate of flow of heat through them will be
A1:1B1:8C2:1D8:1Two wires A and B are of the same maeterial. Their lengths are in the ratio 1 : 2 and the diameters are in the ratio 2 : 1. IF they are pulled by the same force, their increases in length will be in the ratio
A2:1B1:4C1:8D8:1
The lengths of two wires of same material are in the ratio 1:2, their tensions are in the ratio 1:2 and their diameters are in the ratio 1:3. the ratio of the notes they emits when sounded together by the same source is
View SolutionTwo wires A and B of same material have radii in the ratio 2:1 and lengths in the ratio 4:1. The ratio of the normal forces required to produce the same change in the lengths of these two wires is
View SolutionAlcohol flows through two capillary tubes under a pressure lead. The diameter of the two tubes are in the ratio of 4:1 and the length are in the ratio of 1:4. Compare the rate of flow of alcohol through the two tubes.
View SolutionTwo wire mode of the same material are subjected to force in the ratio of 1:2. Their lengths are in the ratio 8:1 and diameters in the raio 2:1. Find the ratio of their extension.
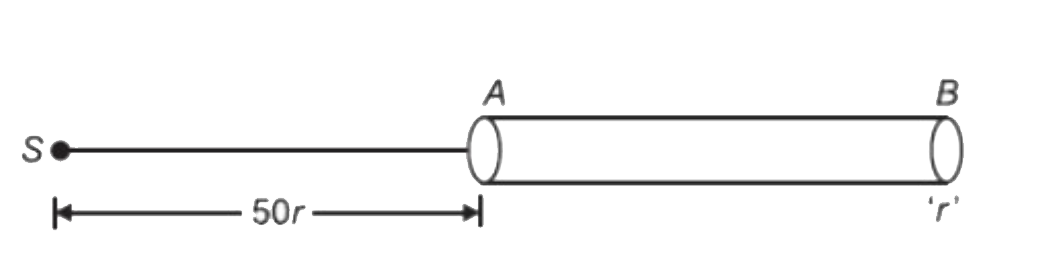
View SolutionA cylindrical rod of length l and cross - sectional radius r is placed at a distance of 50 r from a infrared point source S of power 1.25 kw as shown in the figure. The lateral surface of the rod is perfectly insulated from the surroundings . If the cross - section A absorbs 80 % of the incident energy and the temperature difference between the ends of the rod is constant , then the rate of heat flow through the rod in steady state is
View SolutionTwo wires of the same material have lengths in the ratio 1:2 and their radii are in the ratio 1:√2 If they are stretched by applying equal forces, the increase in their lengths will be in the ratio
View Solution