A thin straight infinitely long conducting wire having charge density λ enclosed bya cylindrical surface of radius rand length lr, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
To find the expression for the electric flux through the surface of a cylindrical surface surrounding an infinitely long conducting wire with a linear charge density λ, we can follow these steps:
1. Identify the Charge Enclosed:
The charge enclosed by the cylindrical surface can be calculated using the linear charge density λ and the length L of the cylinder. The total charge Q enclosed is given by:
Q=λ⋅L
2. Use Gauss's Law:
According to Gauss's Law, the electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
Φ=Qϵ0
3. Substitute the Charge Enclosed:
Now, substituting the expression for Q into the equation for electric flux, we get:
Φ=λ⋅Lϵ0
4. Final Expression:
Thus, the expression for the electric flux through the surface of the cylinder is:
Φ=λLϵ0
The charge enclosed by the cylindrical surface can be calculated using the linear charge density λ and the length L of the cylinder. The total charge Q enclosed is given by:
Q=λ⋅L
According to Gauss's Law, the electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ϵ0:
Φ=Qϵ0
Now, substituting the expression for Q into the equation for electric flux, we get:
Φ=λ⋅Lϵ0
Thus, the expression for the electric flux through the surface of the cylinder is:
Φ=λLϵ0
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[Set- II]
Explore 4 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[Set-III]
Explore 3 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-III, DELHI BOARD
Explore 4 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A cylinder of length L and radius b has its axis coincident with x-axis. The electric field in this region is →E=200ˆi. Find the flux through the left end of the cylinder.
View SolutionConsider a cylindrical surface of radius R and length l in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction.
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionA hollow half cylinder surface of radius R and length l is placed in a uniform electric field →E. Electric field is acting perpendicular on the plane ABCD. Find the flux through the curved surface of the hollow cylindrical surface

View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surface of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surface is .

View SolutionA uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is
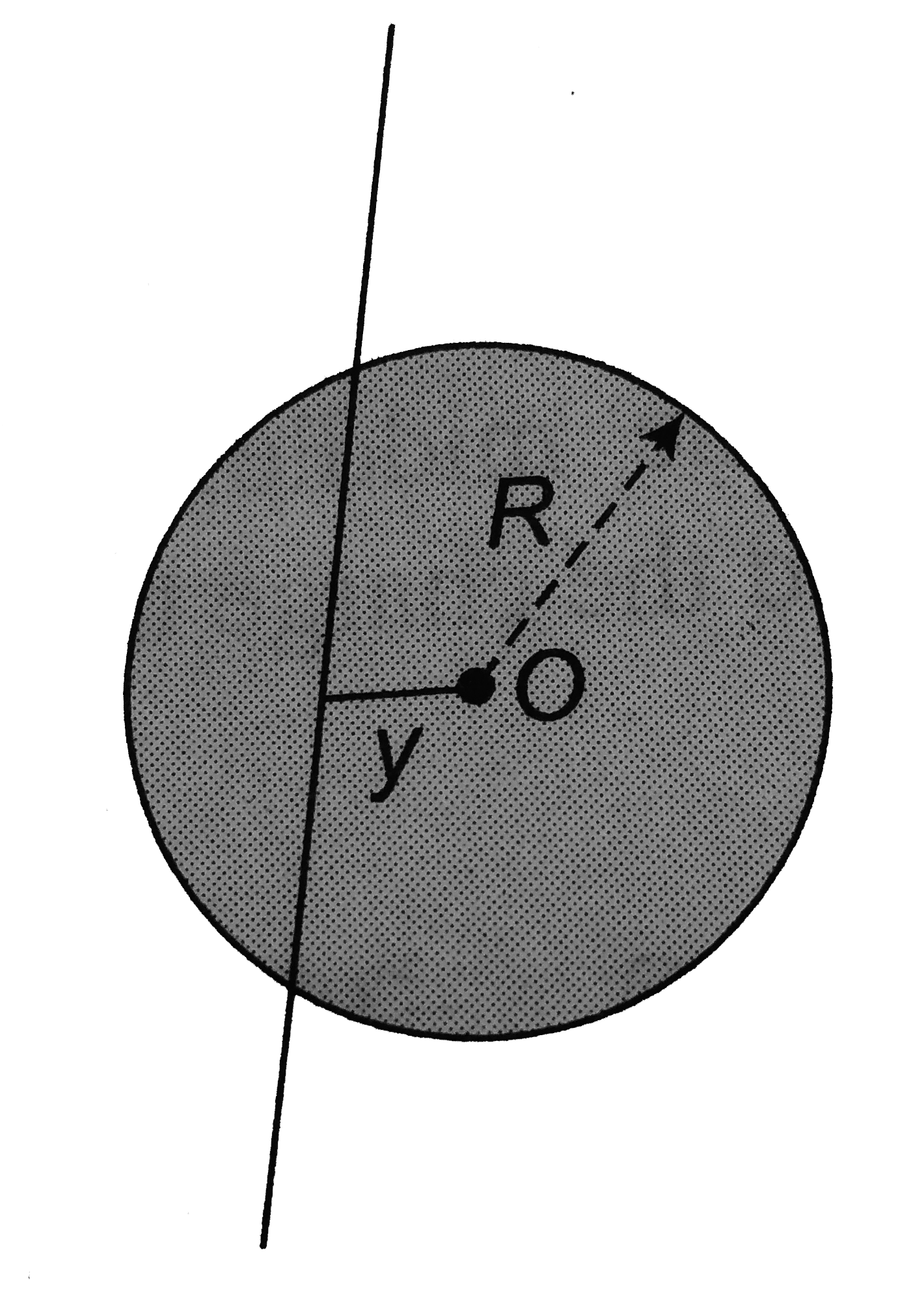
View SolutionA uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is

View SolutionA charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View Solution

