(a)Using Ampere's circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
(b )How is the magnetic field inside a given solenoid made strong?
Step-by-Step Solution
1. Understand the Setup:
- Consider a long solenoid with n turns per unit length, carrying a current I.
- We want to find the magnetic field B at a point inside the solenoid along its axis.
2. Apply Ampere's Circuital Law:
- Ampere's Circuital Law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current Ienc enclosed by the loop:
∮B⋅dl=μ0Ienc
3. Choose an Amperian Loop:
- Consider a rectangular Amperian loop ABCD that passes through the solenoid.
- The sides AB and CD are parallel to the axis of the solenoid, while BC and AD are perpendicular to the magnetic field.
4. Evaluate the Integral:
- The contribution to the integral from sides BC and AD is zero because the magnetic field is perpendicular to these segments:
∫BCB⋅dl=0and∫ADB⋅dl=0
- For sides AB and CD, since they are parallel to B:
∫ABB⋅dl=B⋅land∫CDB⋅dl=0
5. Calculate the Enclosed Current:
- The total current Ienc enclosed by the loop is given by the number of turns enclosed times the current I:
Ienc=n⋅I⋅l
- Here, n is the number of turns per unit length and l is the length of the solenoid that the loop encloses.
6. Combine Results:
- By substituting the evaluated integrals and the enclosed current into Ampere's Law:
B⋅l=μ0(n⋅I⋅l)
- Dividing both sides by l:
B=μ0nI
7. Final Expression:
- Thus, the magnetic field B inside a long solenoid is given by:
B=μ0nI
Part (b): Making the Magnetic Field Inside a Solenoid Stronger
1. Increase the Number of Turns:
- The magnetic field strength can be increased by increasing the number of turns per unit length n. More turns mean more current loops contributing to the magnetic field.
2. Increase the Current:
- Increasing the current I flowing through the solenoid will also increase the magnetic field strength, as B is directly proportional to I.
3. Use of Ferromagnetic Materials:
- Placing a ferromagnetic material (like iron) inside the solenoid enhances the magnetic field. The material becomes magnetized and increases the overall magnetic field strength due to its high permeability.
- Consider a long solenoid with n turns per unit length, carrying a current I.
- We want to find the magnetic field B at a point inside the solenoid along its axis.
- Ampere's Circuital Law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space μ0 times the total current Ienc enclosed by the loop:
∮B⋅dl=μ0Ienc
- Consider a rectangular Amperian loop ABCD that passes through the solenoid.
- The sides AB and CD are parallel to the axis of the solenoid, while BC and AD are perpendicular to the magnetic field.
- The contribution to the integral from sides BC and AD is zero because the magnetic field is perpendicular to these segments:
∫BCB⋅dl=0and∫ADB⋅dl=0
- For sides AB and CD, since they are parallel to B:
∫ABB⋅dl=B⋅land∫CDB⋅dl=0
- The total current Ienc enclosed by the loop is given by the number of turns enclosed times the current I:
Ienc=n⋅I⋅l
- Here, n is the number of turns per unit length and l is the length of the solenoid that the loop encloses.
- By substituting the evaluated integrals and the enclosed current into Ampere's Law:
B⋅l=μ0(n⋅I⋅l)
- Dividing both sides by l:
B=μ0nI
- Thus, the magnetic field B inside a long solenoid is given by:
B=μ0nI
- The magnetic field strength can be increased by increasing the number of turns per unit length n. More turns mean more current loops contributing to the magnetic field.
- Increasing the current I flowing through the solenoid will also increase the magnetic field strength, as B is directly proportional to I.
- Placing a ferromagnetic material (like iron) inside the solenoid enhances the magnetic field. The material becomes magnetized and increases the overall magnetic field strength due to its high permeability.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
The magnetic field inside a solenoid is-
View SolutionUsing Ampere.s Circuital Law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.
View SolutionIn using Ampere's law,to find the magnetic field inside a straight long soleniod the loop that is taken is
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
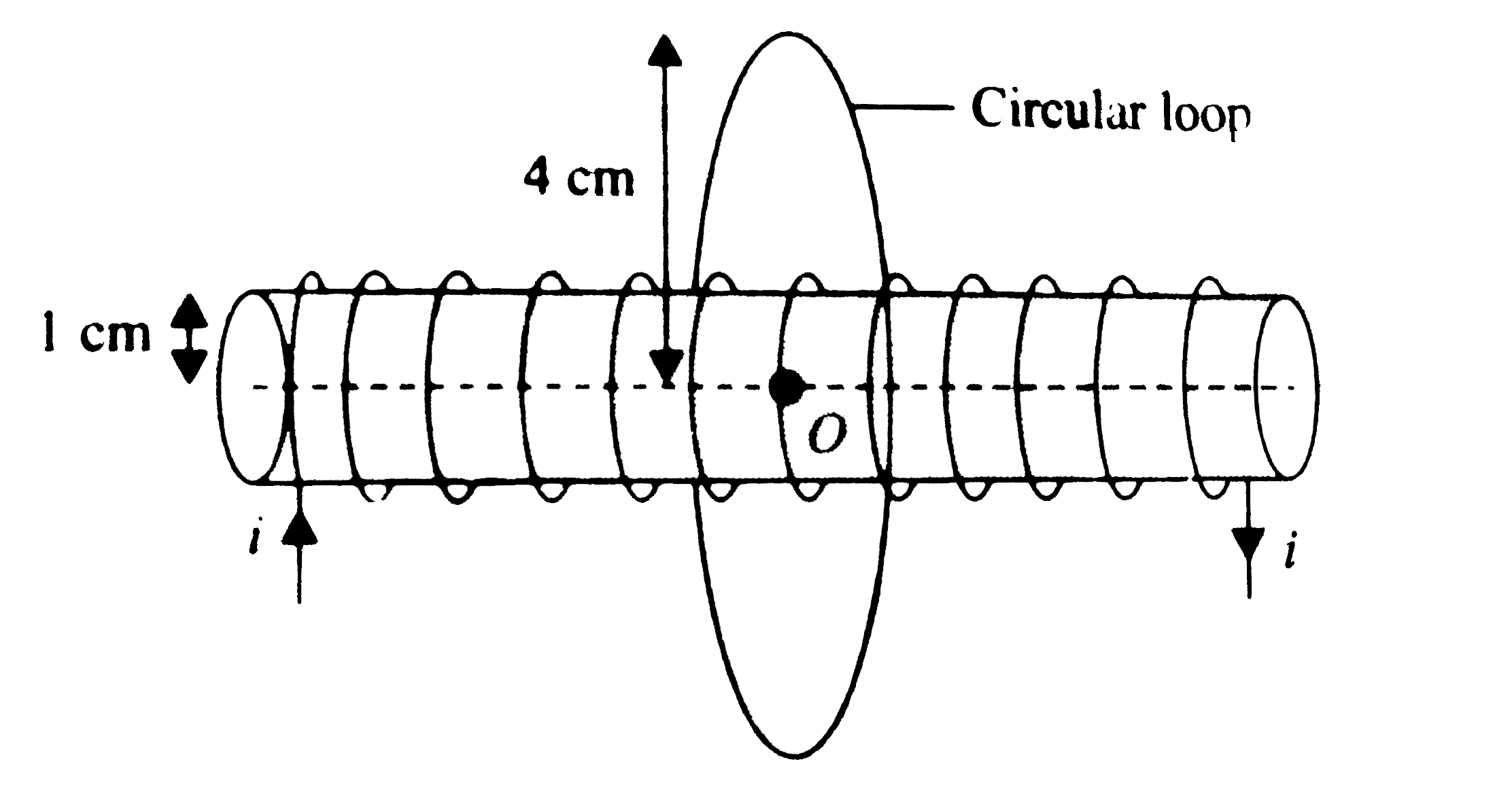
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
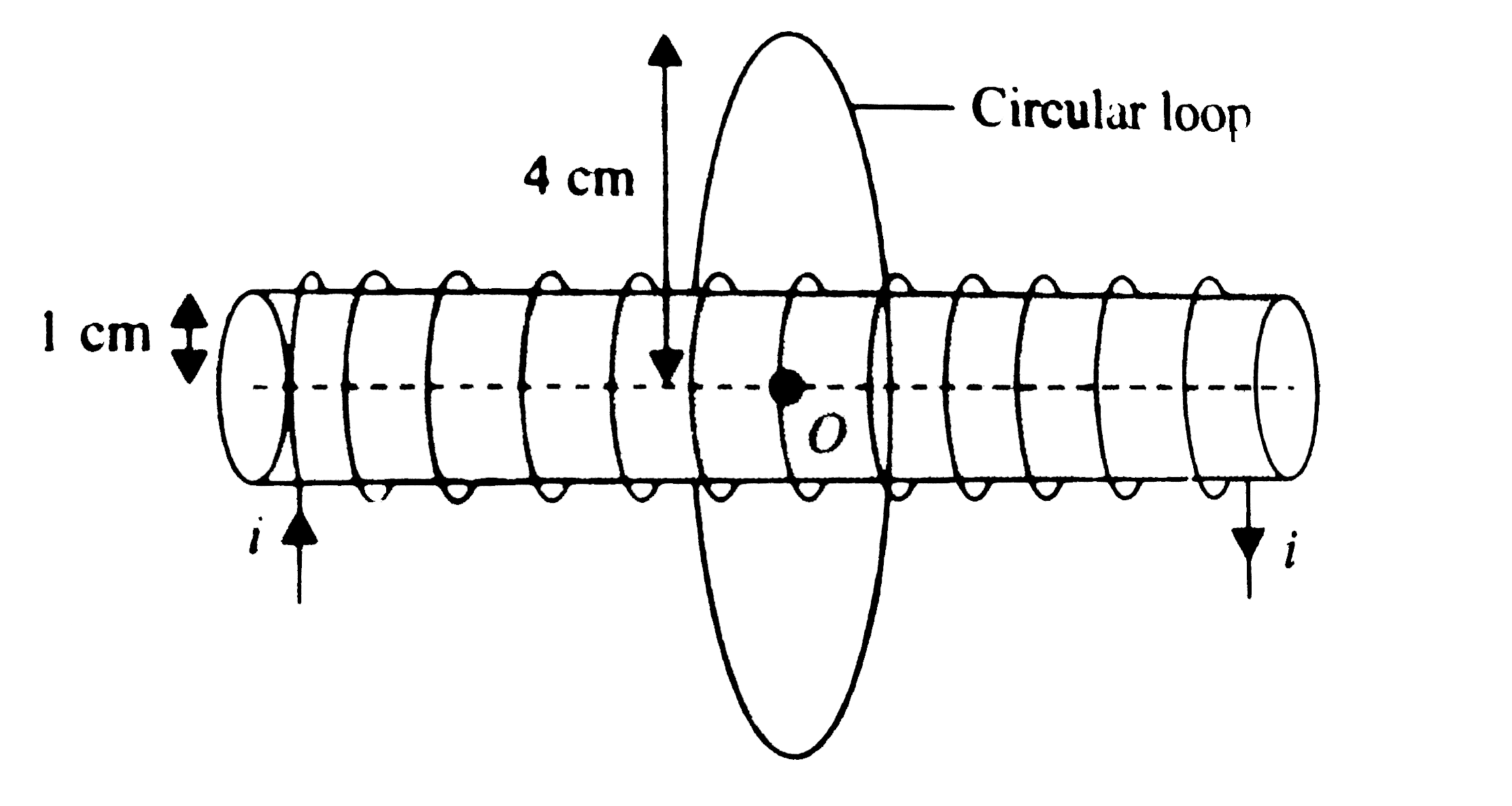
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
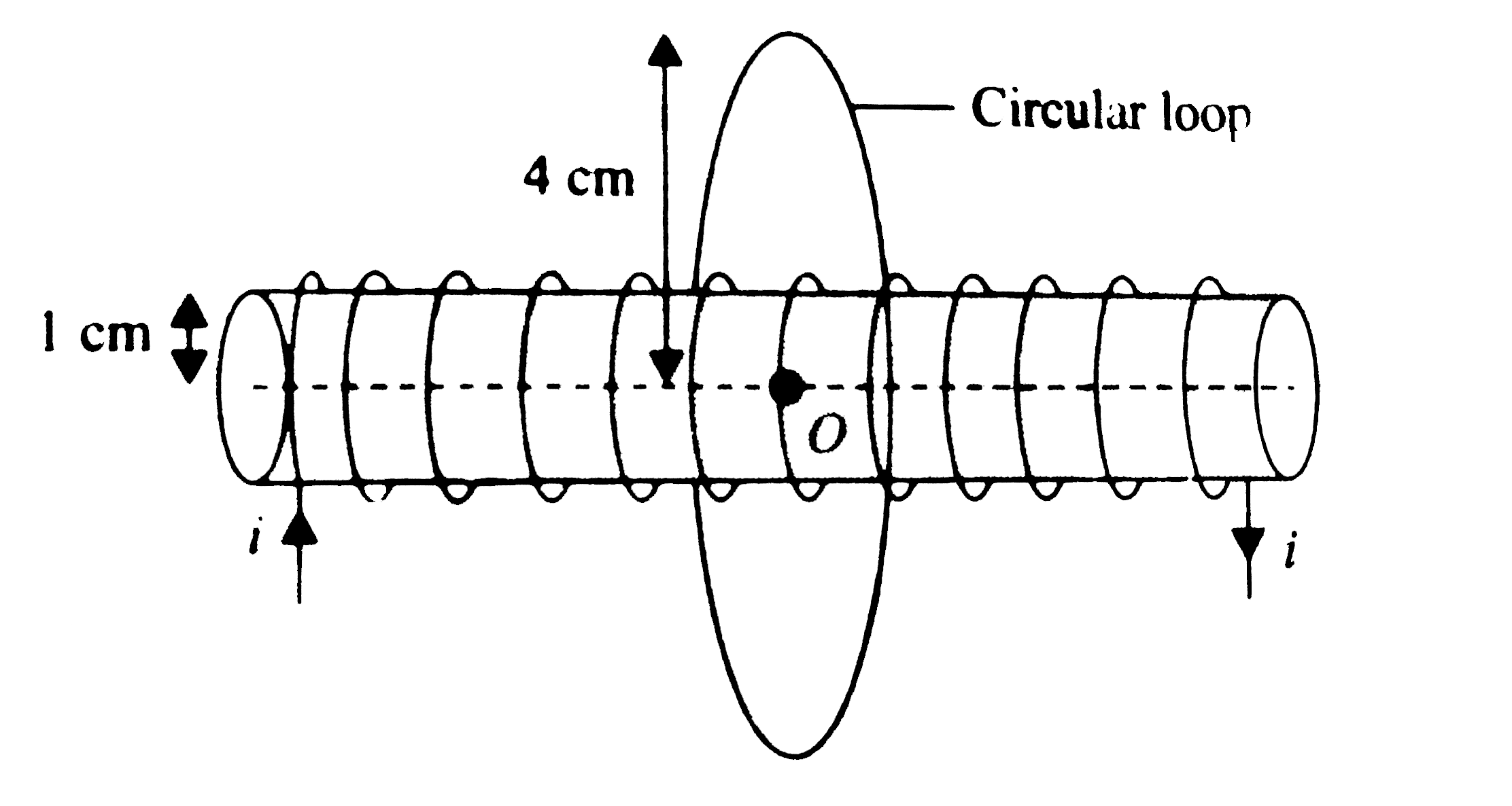
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnitude of induced current that appears in the circular loop is
View SolutionThe strength of magnetic field inside a long current-carrying straight solenoid is:
View Solution(A) : A solenoid tend to contract when a current passes through it.
(R) : The magnetic field inside the solenoid is uniform.
View SolutionUsing Ampere.s circuital law, obtain an expression for the magnetic flux density .B. at a point .X. at a perpendicular distance .r. from a long current carrying conductor. (Statement of the law is not required).
View Solution
